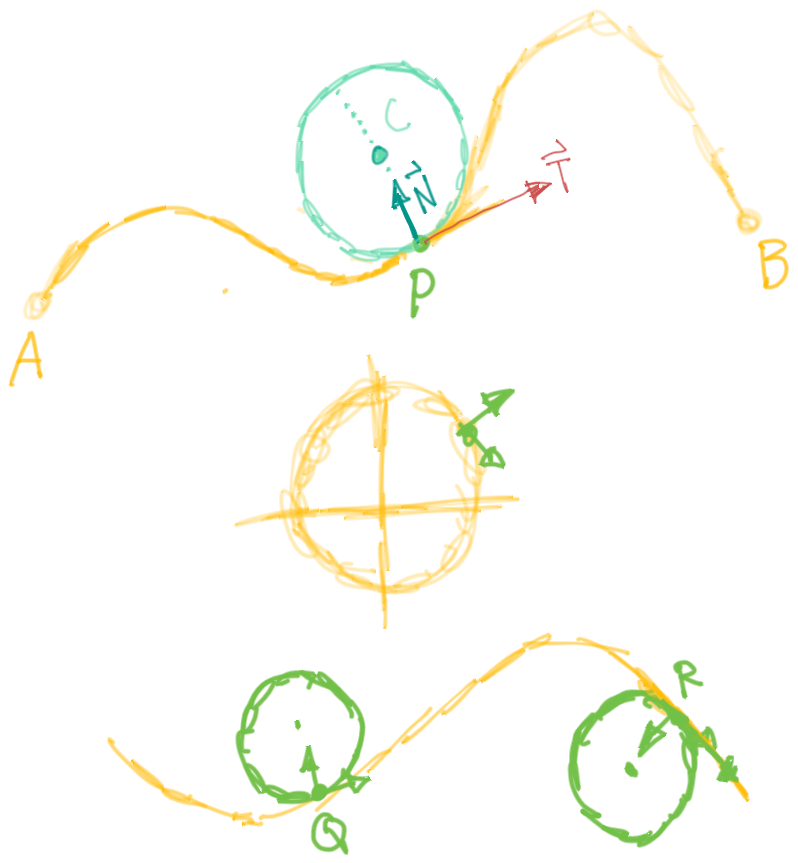Chemistry
Basics
Given some element
Where
- Cations
- Positively (+) Charged
- Anions
- Negatively (−) Charged
Mnemonic
Cations are Pawsitive
Conventions on homework
When a question says, determine the energy of 1 ㏖ of photons, the unit will be ᴶ/㏖.
Units
SI Prefixes
| Value | Prefix | Symbol |
|---|---|---|
| deca | ||
| hecto | ||
| kilo | ||
| mega | ||
| giga | ||
| tera |
| Value | Prefix | Symbol |
|---|---|---|
| deci | ||
| centi | ||
| mili | ||
| micro | ||
| nano | ||
| pico |
Classification of Matter
Overview

Mixtures
Heterogeneous mixture
Where the prefix Hetero- means different

Homogeneous mixture
Where the prefix Homo- means same

The Atom and Nuclear Chemistry
Isotopes and Subatomic Particles
Electrons and Quantum Mechanics
Average Atomic Mass
If the average atomic mass of boron is , what is the percent abundance of boron-11 (mass of ) if the only other isotope is boron-10 (mass of )? Given the formula for average atomic mass:
Therefore in summary, we are given the following known quantities
With the following unknown quantities
And asked to find the percent abundance of boron-11 (). Therefore our equation is
We have two unknowns, but luckily we can use the following fact/relation and therefore express the percent abundance of boron-10 in terms of the percent abundance of boron-11
Therefore
But we aren't done, we have to compute significant figures.
Therefore, we round our answer to 2 sig figs, yielding
Molecules and Compounds
Terms
- Electronegativity
- Can be used to to determine type of bond based on electronegativity difference.
- Ionic Bond
- Covalent Bond
- Polar Covalent Bond
- Sharing of electrons.
- Hydrogen Bond
- Hydrogen is bonded with an electronegative element.
Prefixes
| Prefix | Value |
|---|---|
| mono- | |
| di- | |
| tri- | |
| tetra- | |
| penta- |
| Prefix | Value |
|---|---|
| hexa- | |
| hepta- | |
| octa- | |
| nona- | |
| deca- |
Formula Summary
Formal Charge (Option 1)
Given some element which has number of valance electrons, and a lewis diagram of bonded () electrons and non-bonded () electrons, the formal charge for the given element in the lewis structure is
For the given quantities
Formal Charge (Option 2)
Given some element which has number of valance electrons, and a lewis diagram of some number of bonds () and dots (), the formal charge for the given element in the lewis structure is
For the given quantities
Note: each bond is 2 electrons, but counts as one bond.
Polyatomic Ions
Remembering the number of oxygens
General
Given a set of oxygens in increasing order
Where
For example
Given some element or compound ionically bonded with such
For example
The following table denotes the naming conventions therein
| Prefix | Prefix Meaning (relative to suffix) | Suffix | Oxygen Order | Example | |
|---|---|---|---|---|---|
| Formula | Name | ||||
| Per- | More than | -ate | Highest # | Perchlorate | |
| -ate | Higher # | Chlorate | |||
| -ite | Lower # | Chlorite | |||
| Hypo- | less than | -ite | Lowest # | Hypochlorite | |
Oxygen vs No-Oxygen Comparison
| Prefix | Suffix | Meaning | Example | Name |
|---|---|---|---|---|
| Per- | -ate | or | Persulfate | |
| -ate | Sulfate | |||
| -ite | Sulfite | |||
| Hypo- | -ite | Hyposulfite | ||
| -ide | No oxygennon-metal | Sulfide |
In summary
Per*ate
Greater than
- *ate
- *ite
- Hypo*ite
*ate
Less than
- Per*ate
Greater than
- *ite
- Hypo*ite
*ite
Less than
- Per*ate
- *ate
Greater than
- Hypo*ite
Hypo*ite
Less than
- Per*ate
- *ate
- *ite
Generally
| per-ate | Used in the ion with the largest number of oxygen atoms |
|---|---|
| -ate-ite | Polyatomic ions of oxygen |
| hypo-ite | Used in the ion with the lowest number of oxygen atoms |
| -ide | Non-metal, no oxygens |
Determining The Charge†
Warning
Phosphate () is the only one that violates this rule!
Ionic Lewis Structures
Ionic Lewis Structures
Examples
Notes
- When naming an ionic compound, the name of the cation is followed by the name of the anion. Monatomic anions are named with the ending -ide.
Periodic Properties of the Elements
Note, electron affinity is not the same as electronegativity!
Terms
- Isoelectronic
- Atoms with the same number of electrons.
- Ionization energy
- Predict Metallic Character Based on Periodic Trends
Expanded Octet (Exceptions to the Octet Rule)
All non-metals from period 3 to period 8 of the Periodic Table, can have expanded octets.

Quantum Mechanical Models of the Atom
The Electromagnetic Spectrum

Terms
- Pauli Exclusion Principle
- No two electrons in an atom can have the same four quantum numbers.
- Pauli’s Principle prevents two electrons with the same spin from existing in the same subshell, each subshell will be filled with one spin direction before they are filled with the opposite spin. This is the second of Hund’s Rules.
- Aufbau Principle
- This pattern of orbital filling is known as the aufbau principle (the German word aufbau means “build up”).
- Hund’s rule
- When filling degenerate orbitals, electrons fill them singly first, then with parallel spins.
- I.e. start by filling boxes with single 'upward' arrows, and then once all of such boxes are maxed out, then you add double arrows pointing in opposite directions.
- Pauli’s Principle prevents two electrons with the same spin from existing in the same subshell, each subshell will be filled with one spin direction before they are filled with the opposite spin. This is the second of Hund’s Rules.
- Coulomb’s Law
Aufbau Principle

Hund’s rule

Pauli's Exclusion Principle
Each election has a unique set of four quantum numbers (i.e. see quantum numbers). They are
Overview

Formulas
Values
| Name | Symbol | Unit | Description | Range |
|---|---|---|---|---|
| Wavelength | Any unit for distance | Distance between two analogous points | Always Positive | |
| Frequency | or (nu) | Number of cycles | Always Positive | |
| Energy | (joule) | Amount of energy () in a light packet |
Constants
| Name | Symbol | Unit | Value |
|---|---|---|---|
| Speed of Light | |||
| Planck's constant |
|
Other Formulas
de Broglie Relation
Heisenberg's Uncertainty Principle
Where
- is the uncertainty in position.
- is the uncertainty in velocity.
- is the mass of the particle.
- is the plank's constant.
In general it states that the more you know about an electrons position, the less you know about it's velocity.
Energy of an Electron in an Orbital with Quantum Number in a Hydrogen Atom
Energy of an Electron in an Orbital with Quantum Number for any atom
Where is the atomic number of the given element.
Change in Energy That Occurs in an Atom When It Undergoes a Transition between Levels (Further Details)
and
- If is negative, energy is being released.
- If is positive, energy is being absorbed.
Ionization Energy
Where
- is the electron number
- the point on the table where you see the highest difference/delta.
Atomic Spectroscopy
The Principal Quantum Number (n) (Hydrogen Atom)
For the hydrogen atom, the energy of an electron in an orbital with quantum number is given by
Therefore the difference in energy is given by the following
The Principal Quantum Number (n) (Any Atom)
For the hydrogen atom, the energy of an electron in an orbital with quantum number is given by
TODO
Where is the atomic number of the given element.
Electron Configuration
Examples
Electron configuration for
Since the electron configuration for Argon is
Electron configuration for
Beginning with the electron configuration for
Remove the electrons from the term with the higher electron state. Warning! Do not just remove the electrons from the rightmost term since the rightmost term may be a lower electron state. For instance given
- is in a higher electron state
- is in a lower electron state
Alternatively, to compute the lowest energy orbital, add the principle quantum number () to the The angular momentum quantum number () to get the orbital with the lowest energy. Therefore
Given and
NVM this is an exception to the rule...
TODO move this somewhere else...
As shown
Therefore the electron configuration for is:
Electron configuration for
It would appear that the electron configuration for would be
But this is wrong! It's actually
How-tos
What are the valence electrons?
Given
The valance electrons will be the ones in the highest energy state. Therefore
Therefore there are valence electrons.
Given
The valance electrons will be the ones in the highest energy state. Therefore
Therefore there are valence electrons.
Quantum Numbers
Overview
| Symbol | Description |
|---|---|
| The principle quantum number | |
| The angular momentum quantum number | |
| The magnetic quantum number | |
| The spin quantum number |
The Principle Quantum Number ()
| Value of | Value of | Orbital Sublevel |
|---|---|---|
Angular Momentum Quantum Number
| Value | Result |
|---|---|
| Value of | Value of |
|---|---|
Summary
Useful Formulas
The equation for a maximum number of electrons a given energy level can hold given some value for
How many orbitals are possible given some value for
Examples



Light
Interference and Diffraction
Constructive Interference
If two waves of equal amplitude are in phase when they interact—that is, they align with overlapping crests—a wave with twice the amplitude results. This is called constructive interference.

Destructive Interference
If two waves are completely out of phase when they interact—that is, they align so that the crest from one overlaps with the trough from the other—the waves cancel by destructive interference.

Mathematics
Algebra
Miscellaneous
Functional Utilities & Notation Conveniences
Right to Left Evaluation
Left to Right Evaluation
Derivative Shorthand
For this notation, the derivative with respect to a given variable, is implicit.
Radians & Radian Conversion
Constants
Algebra
Properties
Trigonometry
The Unit Circle & Special Angles In Trig

Warning
Never use Pi ()! It makes (thinking in terms of) radians confusing, Tao () is what the enlightened trigonometer uses, and won't screw you over.
To easily memorize the special angles in trig, notice the repeating patterns on the above angles.
- For values on the x-axis, anything over and under will be negative
- For values on the y-axis, anything over will be negative
-
Diagonals will be , For ratios of on the sides, i.e.
,
,
,
,
,
,
, and
.
Draw a circle and dot the point where it occurs (which is pretty easy since the above are simple ratios of a circle when expressed in terms of ). Then with regards to the and axis values:
- The longer size will be
- The shorter side will be
Trigonometric Identities
Pythagorean Identities
Sum and Difference Identities
Cofunction Identities
Ratio Identities
Double-Angle Identities
Half-Angle Identities
Power-Reducing Identities
Product-to-Sum Identities
Sum-to-Product-Identities
Trigonometric Equations
Coordinate & Number Systems
Polar Coordinate System
Given
Then
Properties
Given
Then
De Moivre’s Theorem
De Moivre’s Theorem For Finding Roots
Trigonometric form of a complex number
Vectors
Quick Facts
Two vectors are equal if they share the same magnitude and direction.
Initial points don't matter. You can define a vector with two points.
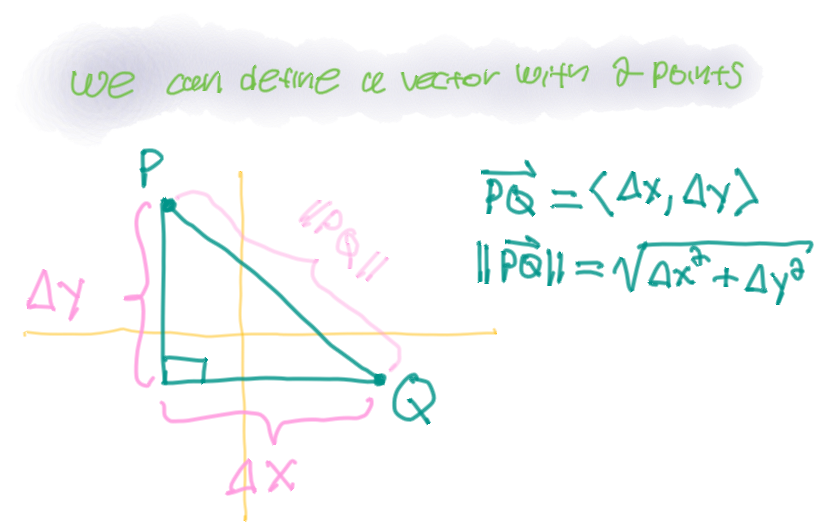
Do not divide vectors!
Vector Operations
Dot Product
Cross Product
Length of a Vector
Definition of Vector Addition
If and are positioned so the initial point of is at the terminal point of , then the sum is the vector from the initial point of to the terminal point of .
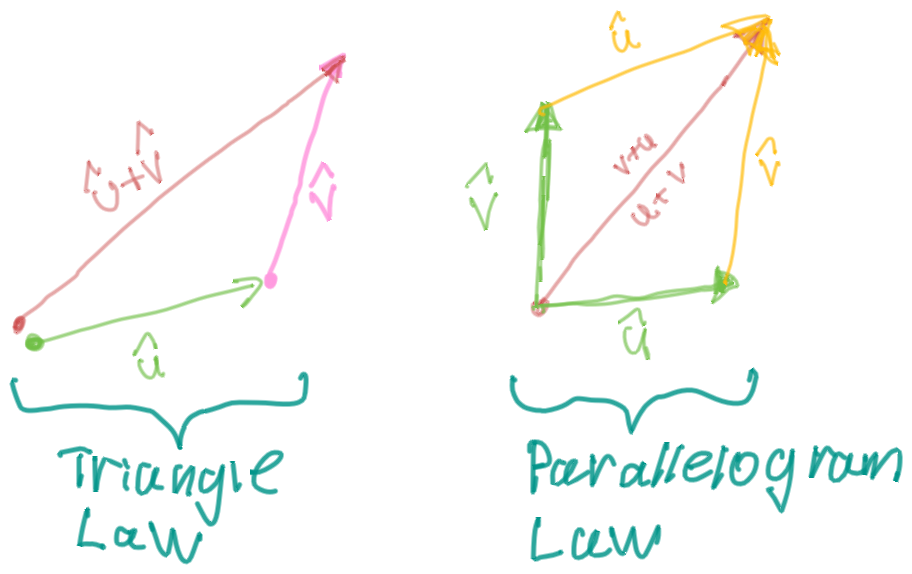
Given some vectors and , the vector is the vector that points from the head of to the head of
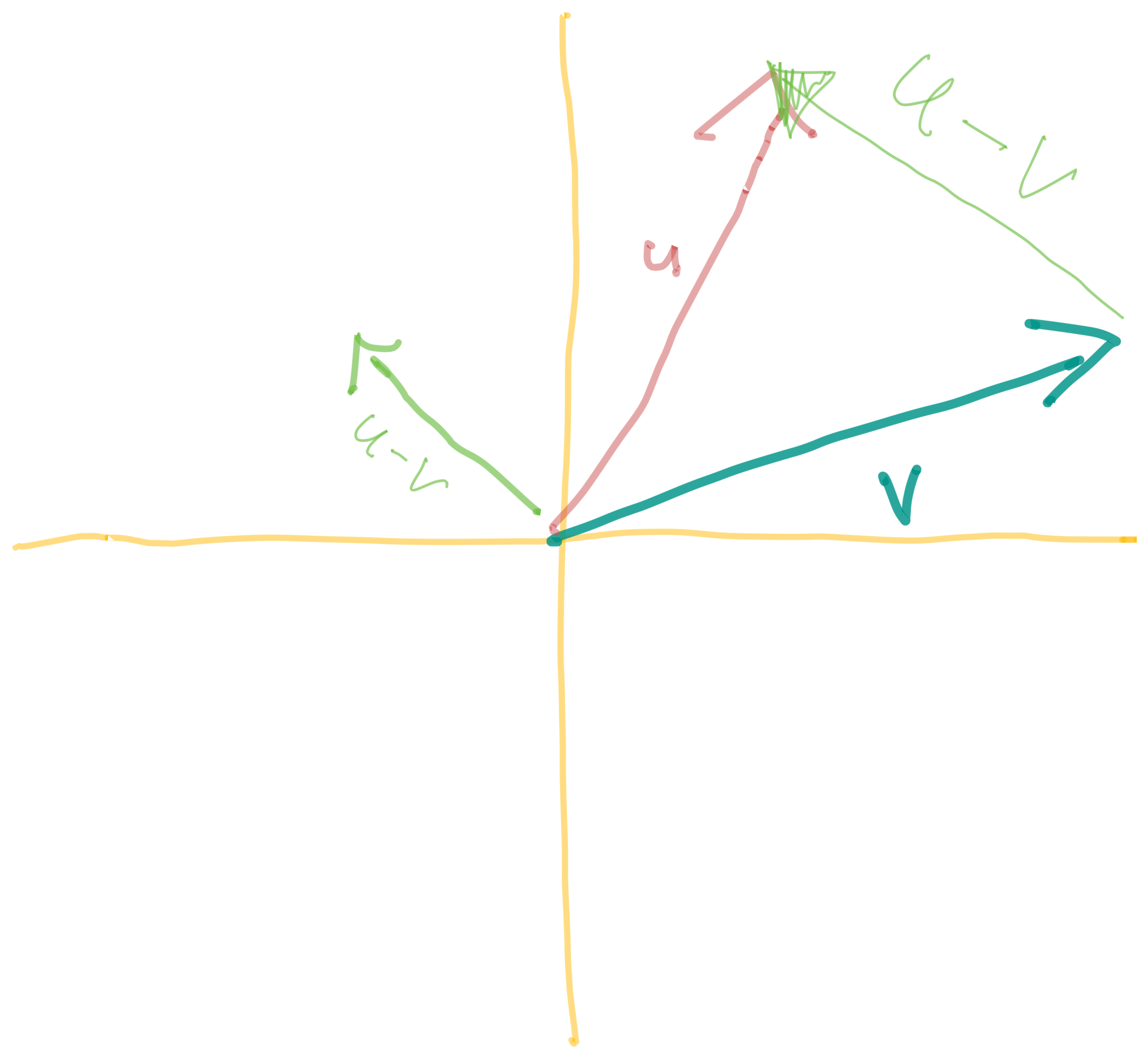
Standard Basis Vectors
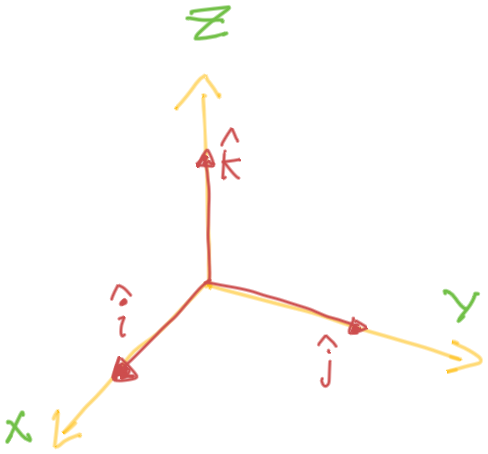
Orthogonal
Two vectors are orthogonal if and only if
The Unit Vector
If is the angle between the vectors and , then
If is the angle between the nonzero vectors and , then
Two nonzero vectors and are parallel if and only if
Properties of the Dot Product
Direction Cosines & Direction Angles of a Vector
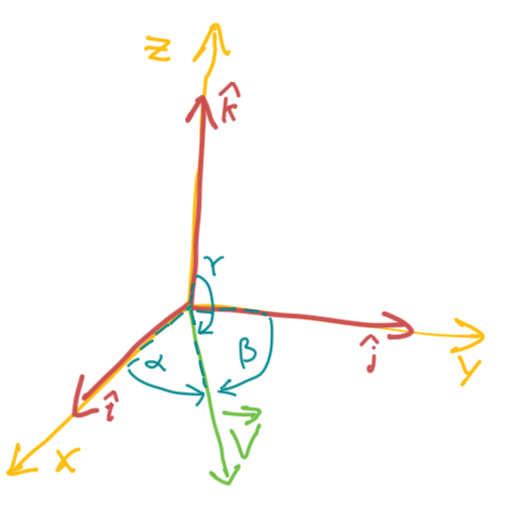
Where
Vector Relations
Parallel Vectors
- When two vectors are parallel; they never intersect (duh).
Given some vectors
The vectors and are parallel if and only if they are scalar multiples of one another.
Alternatively
Orthogonal Vectors
- When two vectors are orthogonal; they meet at right angles.
Given some vectors
Two vectors are orthogonal if and only if
Reparameterization of the position vector in terms of length
- We can parametrize a curve with respect to arc length; because arc length arises naturally from the shape of the curve and does not depend on any coordinate system.
The Arc Length Function
Given
We can redefine in terms of arc length between two endpoints
That is, is the length of the curve () between and .
Furthermore from the adjacent definition; we can simply the above to
The Arc Length Function
That is
Vectors Derived From Some Curve Defined by
The Unit Tangent Vector
The Unit Normal Vector
The Binormal Vector
- Therefore, the binormal vector is orthogonal to both the tangent vector and the normal vector.
- The plane determined by the normal and binormal vectors N and B at a point P on a curve C is called the normal plane of C at P.
- The plane determined by the vectors T and N is called the osculating plane of C at P. The name comes from the Latin osculum, meaning “kiss.” It is the plane that comes closest to containing the part of the curve near P. (For a plane curve, the osculating plane is simply the plane that contains the curve.)
Kappa - Curvature of a Vector
Tangential & Normal Components of the Acceleration Vector of the Curve
When we study the motion of a particle, it is often useful to resolve the acceleration into two components, one in the direction of the tangent and the other in the direction of the normal.
Specifically
Vector Calculus
The Position Vector
(Original Function)
The Velocity Vector
(First Derivative)
- The velocity vector is also the tangent vector and points in the direction of the tangent line.
- The speed of the particle at time t is the magnitude of the velocity vector, that is,
The Acceleration Vector
(Second Derivative)
Matrices
Reference
The Determinant of A Matrix
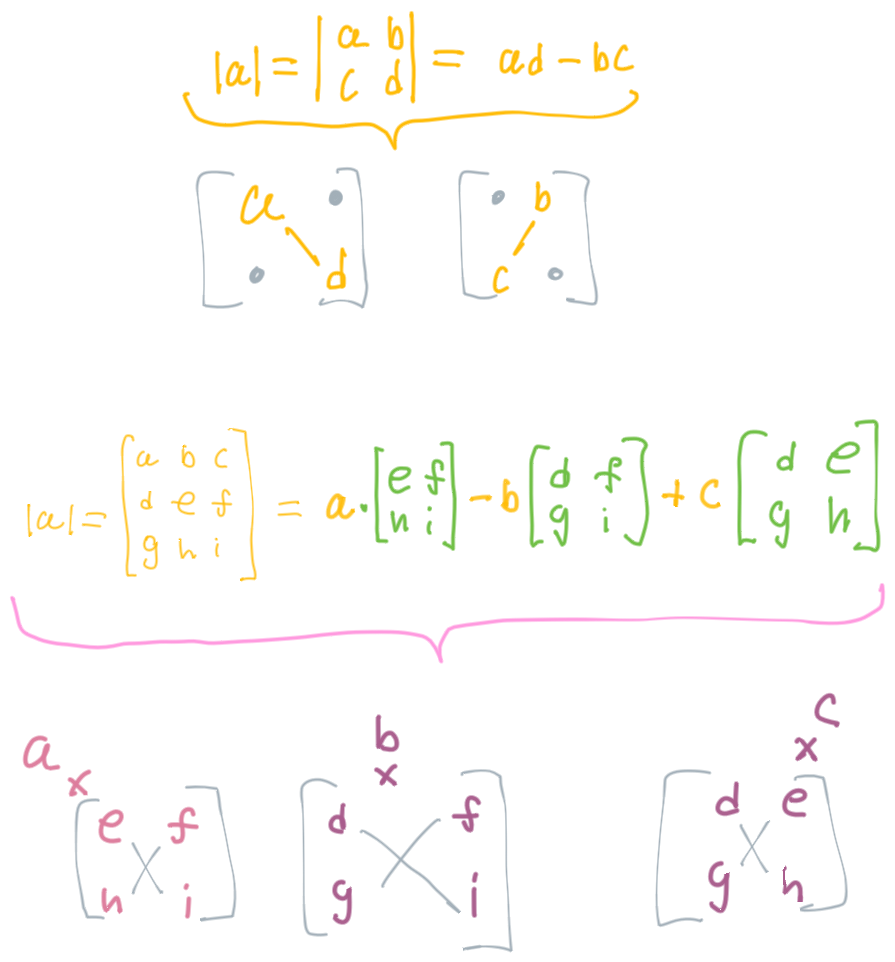
Only works for square matrices.
The Cross Product
Geometry
Definition of a Line
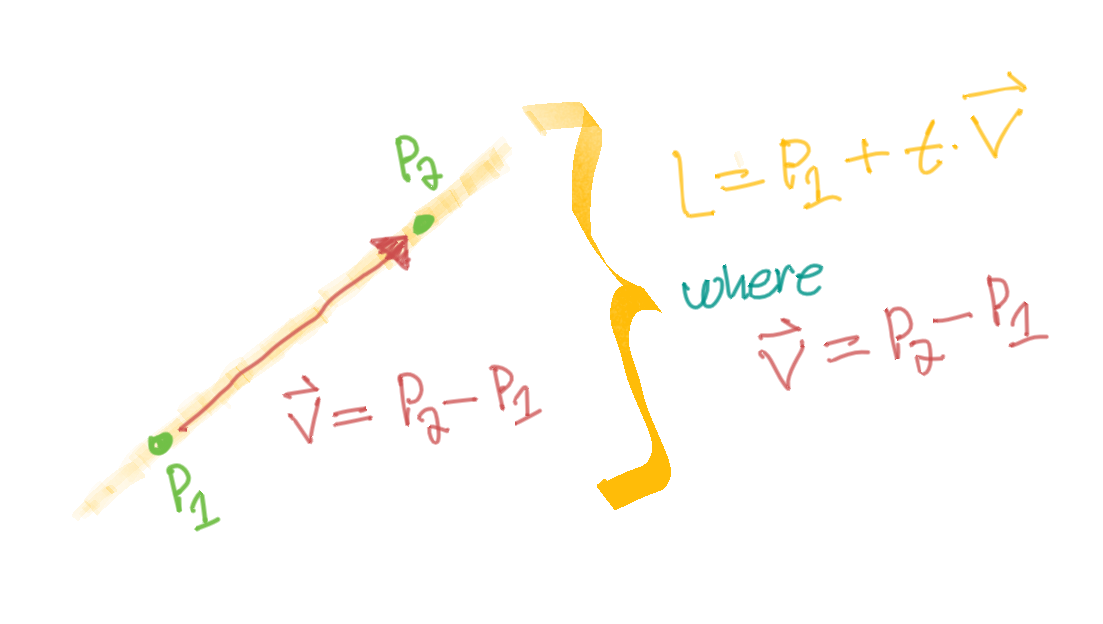
Vector Equation of a Line
Given
We can define a vector between and
Therefore
The equation of a line in 3D space or can be defined VIA the following options
That is
Parametric Equation of a Line
Essentially
That is, is the scaling factor. In a way, it's like it's a function of , but also similar to the slope () in , except (i.e. ) is parameterized.
Sometimes this will be (confusingly) denoted as
Symmetric Equation of a Line
Therefore
Rationale
We rewrite in terms of .
That is
Parameterizations of a curve
- Parametrized curve
- A curve in the plane is said to be parameterized if the set of coordinates on the curve, (x,y), are represented as functions of a variable t.
- A parametrized Curve is a path in the xy-plane traced out by the point as the parameter ranges over an interval .
- A parametrized Curve is a path in the xyz-plane traced out by the point as the parameter ranges over an interval .
Curvature Properties
Length of a Curve
The Arc Length Function
Suppose
- Given some curve defined by some vector in
- where is continuous and is traversed exactly once as increases from to
We can define it's arc length function VIA
Calculus
Derivative Tables
Integration Tables
Riemann Sums
Given
Midpoint Riemann Sum
We can also do away with the index notation and simplify things.
Trapezoidal Riemann Sum
Simpson's Rule
Infinite Sequences
Infinite Series
Infinite Series
Note that the limit of every convergent series is equal to zero. But the inverse isn't always true. If the limit is equal to zero, it may not be convergent.
For example, does diverge; but it's limit is equal to zero.
If the limit is equal to zero; the test is inconclusive.
Geometric Series
Given
Alternatively
Tests
Furthermore
The Integral Test
Constraints on
- Continuous
- Positive
- Decreasing (i.e. use derivative test)
P-Series -or- Harmonic Series
Note: the Harmonic series is the special case where
Comparison Test
Limit Comparison Test
Warning
- If , this only means that the limit comparison test can be used. You still need to determine if either or converges or diverges.
- Therefore, this does not apply to any arbitrary rational function.
Notes
- For many series, we find a suitable comparison, , by keeping only the highest powers in the numerator and denominator of .
Estimating Infinite Series
Differential Equations
Separable Differential Equations
Growth and Decay Models
The above states that all solutions for are of the form .
Where
Exponential growth occurs when , and exponential decay occurs when .
The Law of Natural Growth:
The Logistic Model of Population Growth:
Where
Solving the Logistic Equation
Via partial fraction decomposition
Rewriting the differential equation
Second Order Homogeneous Linear Differential Equations with Constant Coefficients
Properties
If and are solutions; then is also a solution. Therefore, the most general solution to some second order homogeneous linear differential equations with constant coefficients would be .
This is why, when you find two solutions to the characteristic equation and respectively, we write it like so.
Given some:
We can presume that is of the form , and therefore:
Substituting this back into the original equation, we have:
Where:
So therefore:
Where the general solution is of the form:
Parametric Equations
First Derivative Formula
To find the derivative of a given function defined parametrically by the equations and .
Second Derivative Formula
To find the second derivative of a given function defined parametrically by the equations and .
Given
Therefore
The above shows different ways of representing . (I.e. it doesn't correspond to some final solution.)
Arc Length
Formula for the arc length of a parametric curve over the interval .
Physics
Kinematic Equations in 1D
Standard Equations
Summary
| Formula | Missing | Quantities Present |
|---|---|---|
Deriving Displacement Formulas
Displacement when object moves with constant velocity
Deriving

Displacement when object accelerates from rest
Deriving

Deriving The Other Kinematic Formulas
Deriving
Given
We can rearrange from equation (1) like so
Therefore
Deriving
Given
from equation (1) can be rearranged as
from equation (2) can be rearranged like so
Using the following equations from above
- from equation (3)
- from equation (4)
Rearranging equation (5)
Rearrange again to obtain the more common form
TODO
Two-dimensional Projectile Motion
Summary


It's easy to see in the above visualization that and increase linearly, while is non-linear.


Formulas
Displacement & Projectile Position
Generalized
In general (without respect to any or axis values)
Where the distance traveled or displaced is
In terms of and axis values
With respect to the axis
The displacement of a given projectile in terms of the axis is
Since
Which can be read as (in terms of the axis)
With respect to the axis
The displacement of a given projectile in terms of the axis is
Note that (because there is no force acting on the projectile in the horizontal direction), and therefore the initial and final velocities are the same. I.e. it's constant throughout. Therefore in summary
- and therefore we will simple refer to the velocity vector as as .
Therefore we can simplify equation (1) considerably
Solving Projectile Motion Problems
Projectile Motion

In terms of the axis
TODO
TODO
In terms of the axis
TODO
TODO
In Summary
Initial Quantities
Derived expressions
Solutions
Projectile Motion from an initial height, with given initial velocity and angle

Given
- A projectile angle
- The initial height
- The initial velocity
We can therefore derive the the initial velocities for and in terms of the given angle and initial velocity.
Given the general formulas for displacement and velocity
Which this information, we will derive specific equations in terms of the and axes governing the projectile.
In terms of the axis
Deriving displacement as a function of time
Using the general formula from above in terms of as a function of time.
Which we can simplify using the following facts
- From the given depiction of the problem, we know that .
- There is no acceleration along the axis, so .
- as shown above.
Therefore
Deriving velocity
In terms of the axis
Deriving displacement as a function of time
Using the general formula from above in terms of as a function of time.
Which we can simplify using the following facts
- Initial height is given to us which we will represent as , for the sake of generality.
- Acceleration along the axis is the constant for gravity, so .
- as shown above.
Therefore
Deriving velocity
In summary
To find the range
We know that at the moment of impact , therefore we can use equation
Rearranging a bit and setting , we can see that solving for will yield the time at which .
Therefore
Plugging the solution for (and ignoring the negative or non-real solutions for ) into will yield the horizontal displacement (range) at the time . Therefore:
To find the maximum vertical displacement (i.e. peak height)
We begin with equation
We know that at the moment our projectile crests its trajectory, the vertical component of our projectile will be zero. Therefore . To find the time, we simply solve for .
Therefore, knowing the time at which our projectile crests its trajectory, we simply plugin our solution for into the function given in equation . I.e:
To find the velocity at a given moment of time
Given some time which we will denote as , to find the velocity we simply plug in our given values for and into equations and . I.e.
With the given value for , yielding the vector at time , which we will denote as
To define the vector in terms of engineering notation, (i.e. )
To define the vector in terms of magnitude (which we will denote as ) and direction (which we will denote as )
Range
The distance a projectile travels is called its range.
Only applies in situations where the projectile lands at the same elevation from which it was fired.

Reasoning About Projectile Motion


Notes
- An object is in free fall when the only force acting on it is the force of gravity.

Question
Based on the figure, for which trajectory was the object in the air for the greatest amount of time?
Answer
Trajectory A
Explanation
All that matters is the vertical height of the trajectory, which is based on the component of the initial velocity in the vertical direction (). The higher the trajectory, the more time the object will be in the air, regardless of the object's range or horizontal velocity.
Problems

The function in this graph represents an object that is speeding up, or accelerating at a constant rate.
When you throw a ball directly upward, what is true about its acceleration after the ball has left your hand?
Answer: The ball’s acceleration is always directed downward.
Wrong: The ball’s acceleration is always directed downward, except at the top of the motion, where the acceleration is zero.
- Question
- As an object moves in the x-y plane, which statement is true about the object’s instantaneous velocity at a given moment?
- Answer
- The instantaneous velocity is tangent to the object’s path
- Wrong
- The instantaneous velocity is perpendicular to the object’s path.
- The instantaneous velocity can point in any direction, independent of the object’s path.
- Explanation
- As an object moves in the x-y plane the instantaneous velocity is tangent to the object‘s path at a given moment. This is because the displacement vector during an infinitesimally small time interval is always directed along the object’s path and the velocity vector always has the same direction as the displacement vector.
Relative Motion
Galilean transformation of velocity
The velocity of some object P as seen from a stationary frame must be the sum of and
Where
| Symbol | Description |
|---|---|
| Velocity as measured in a stationary frame | |
| Velocity of an object measured in the moving frame relative to the moving frame | |
| velocity of the moving frame - with respect to the stationary frame |
Galilean transformation of velocity (alternate notation)
Given two reference frames \text{ A } and and some object . The velocity of the object can be defined in terms of or as shown
| Symbol | Description |
|---|---|
| The velocity of relative to | |
| The velocity of relative to | |
| The velocity of relative to | |
| The velocity of relative to . It locates the origin of relative to the origin of . |
Therefore
Rotational Motion & Kinematics
Basics
Auxiliary Formula Reference
| Formula | Missing | Quantities Present |
|---|---|---|

A particle moves with uniform circular motion if and only if its angular velocity V is constant and unchanging.
Uniform Circular Motion
Uniform means content speed
Forces and Newton's laws of motion
Newton's laws of motion
Normal force and contact force
Balanced and unbalanced forces
Inclined planes and friction
Tension
Test Page
Hello world
Hello world
Hello world
Hello world
Hello world
Hello world
Math
Drawings
Top-Level Title
Top-level Title
Subsection Title
Some Drawing Entry
Some Other Drawing Entry
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat.
Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor.
- Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa.
- Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa.
- Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa.
- Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa.
- Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa.
- Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor.
Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
- Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa.
- Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa.
- Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa.
- Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa.
- Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa.
- Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus.
Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor.
Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.
Hello world
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam a nisi eu sapien bibendum scelerisque. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Fusce id blandit lacus, at interdum massa. Aenean a purus aliquam justo varius feugiat. Quisque eget posuere odio, mollis consectetur purus. Morbi iaculis porta diam, quis rhoncus orci dictum tempor. Pellentesque viverra quam erat, sagittis luctus nulla condimentum in. Morbi dui ligula, laoreet eget urna sed, accumsan semper metus. Orci varius natoque penatibus et magnis dis parturient montes, nascetur ridiculus mus. Mauris ex enim, dapibus vitae sollicitudin vitae, placerat et lorem. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam vel viverra ante. Ut ac lacus erat. Nunc eleifend elementum ex a posuere.