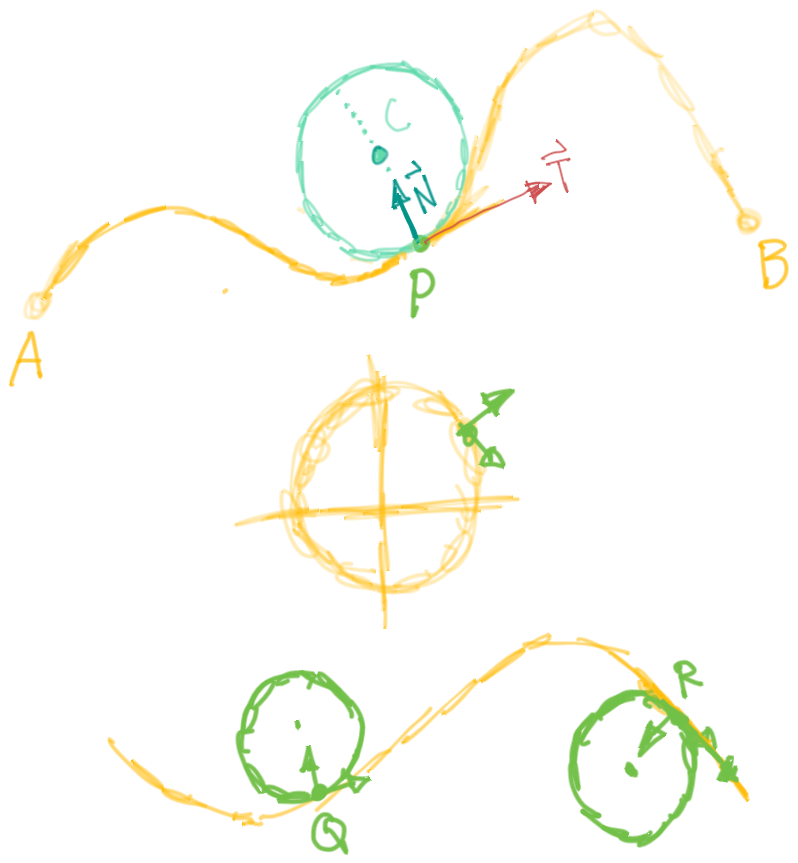For this notation, the derivative with respect to a given variable, is implicit.

Radians & Radian Conversion

Constants

Conversion

Constants

ℯ （Euler's number）

Algebra

Properties

Trigonometry

The Unit Circle & Special Angles In Trig

Warning

Never use Pi （）! It makes （thinking in terms of） radians confusing, Tao （） is what the enlightened trigonometer uses, and won't screw you over.

To easily memorize the special angles in trig, notice the repeating patterns on the above angles.

For values on the x-axis, anything over and under will be negative
For values on the y-axis, anything over will be negative
Diagonals will be , For ratios of on the sides, i.e. , , , , , , , and . Draw a circle and dot the point where it occurs （which is pretty easy since the above are simple ratios of a circle when expressed in terms of ）. Then with regards to the and axis values:
- The longer size will be
- The shorter side will be
See the above examples.

Trigonometric Identities

Pythagorean Identities

Sum and Difference Identities

Cofunction Identities

Ratio Identities

Double-Angle Identities

Half-Angle Identities

Power-Reducing Identities

Product-to-Sum Identities

Sum-to-Product-Identities

Trigonometric Equations

Euler's Formula

Coordinate & Number Systems

Polar Coordinate System

Given

Then

Properties

Given

Then

De Moivre’s Theorem

De Moivre’s Theorem For Finding Roots

Trigonometric form of a complex number

Vectors

Quick Facts

Two vectors are equal if they share the same magnitude and direction.
Initial points don't matter.
You can define a vector with two points.
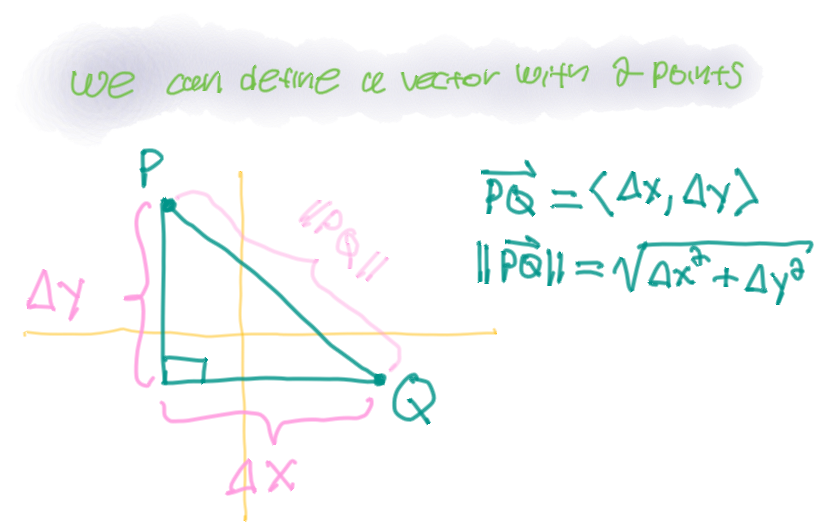
Do not divide vectors!

Vector Operations

Dot Product

Cross Product

Length of a Vector

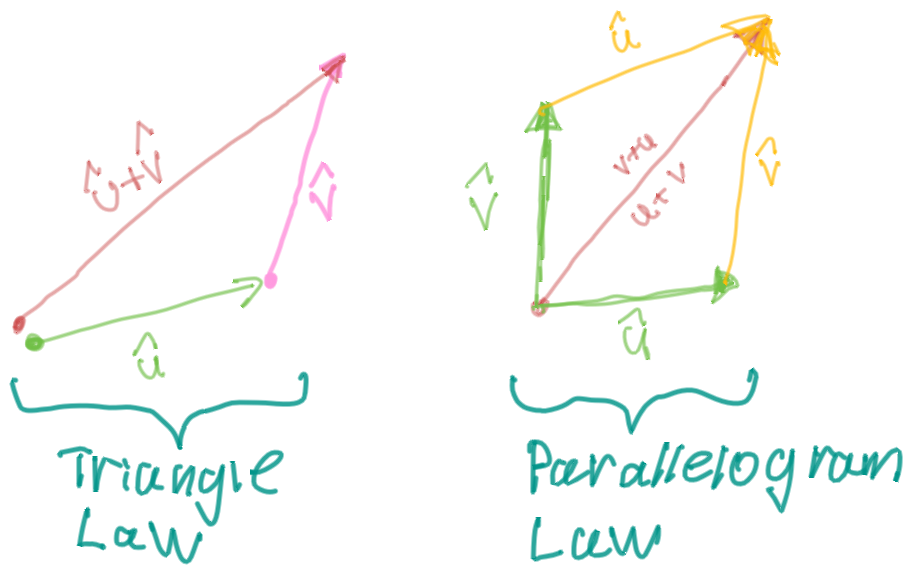
Definition of Vector Addition

If and are positioned so the initial point of is at the terminal point of , then the sum is the vector from the initial point of to the terminal point of .

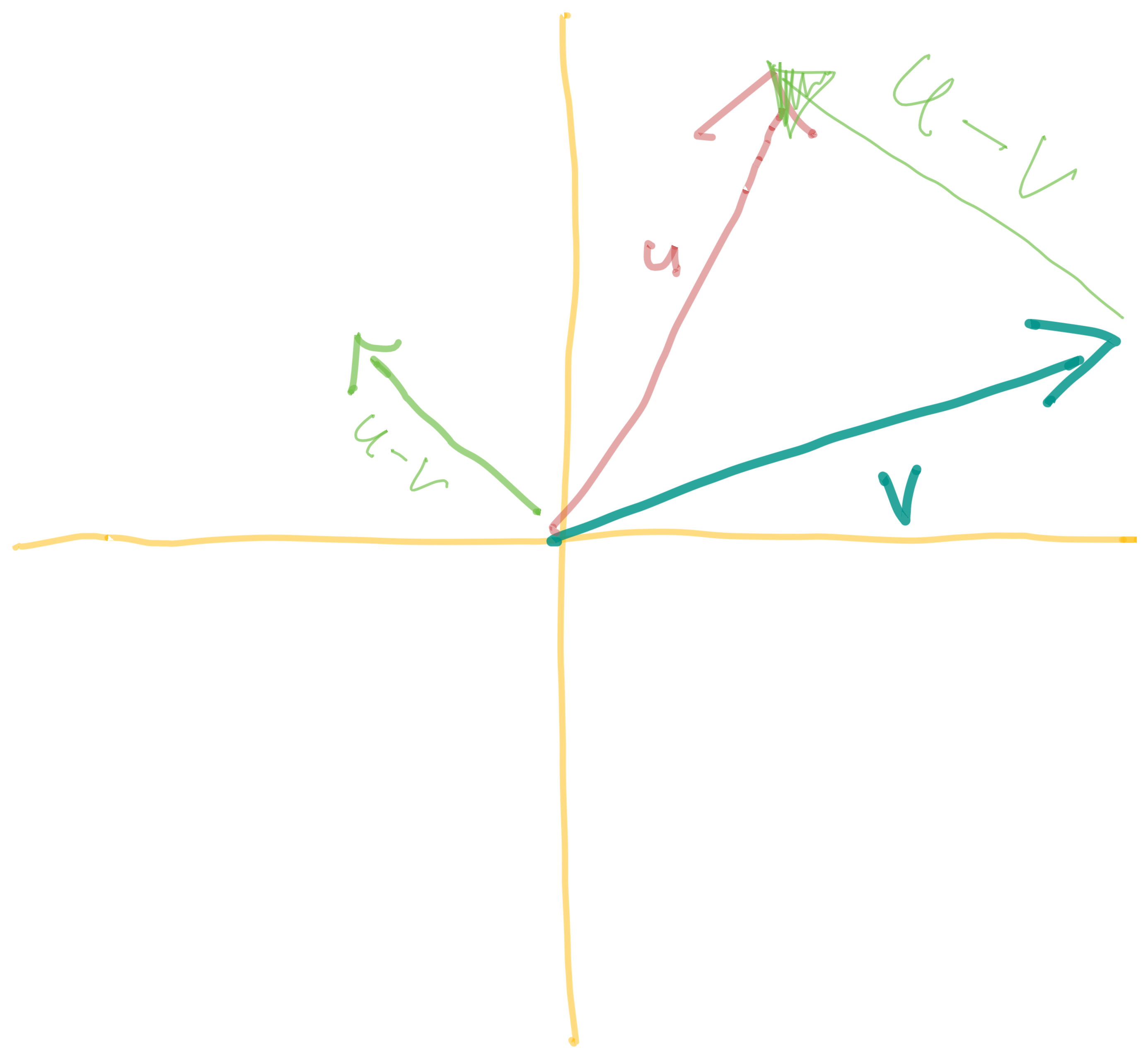
Given some vectors and , the vector is the vector that points from the head of to the head of

Standard Basis Vectors

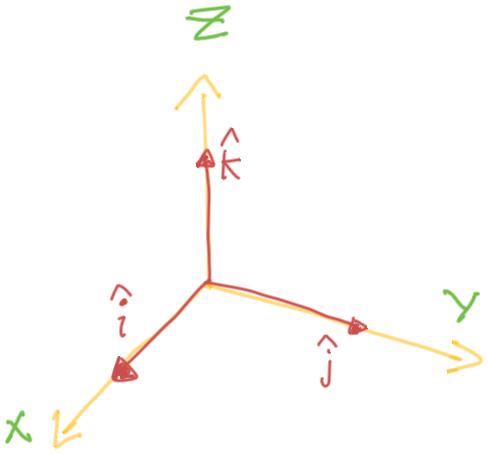
Orthogonal

Two vectors are orthogonal if and only if

The Unit Vector

If is the angle between the vectors and , then

If is the angle between the nonzero vectors and , then

Two nonzero vectors and are parallel if and only if

Properties of the Dot Product

Direction Cosines & Direction Angles of a Vector

Where

Direction Cosines

Direction Angles

Theorem

Proof

Given

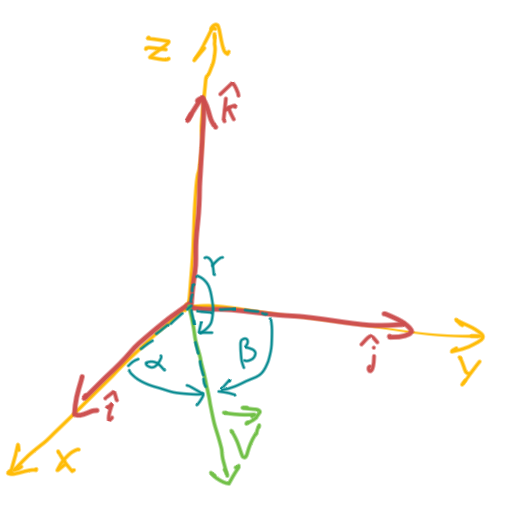
Therefore

Vector Relations

Parallel Vectors

When two vectors are parallel; they never intersect （duh）.

Given some vectors

The vectors and are parallel if and only if they are scalar multiples of one another.

Alternatively

Orthogonal Vectors

When two vectors are orthogonal; they meet at right angles.

Given some vectors

Two vectors are orthogonal if and only if

Reparameterization of the position vector in terms of length

We can parametrize a curve with respect to arc length; because arc length arises naturally from the shape of the curve and does not depend on any coordinate system.

The Arc Length Function

Given

We can redefine in terms of arc length between two endpoints

That is, is the length of the curve （） between and .

Furthermore from the adjacent definition; we can simply the above to

The Arc Length Function

That is

Vectors Derived From Some Curve Defined by

The Unit Vector

The Unit Tangent Vector

The Unit Normal Vector

The Binormal Vector

Therefore, the binormal vector is orthogonal to both the tangent vector and the normal vector.
The plane determined by the normal and binormal vectors N and B at a point P on a curve C is called the normal plane of C at P.
The plane determined by the vectors T and N is called the osculating plane of C at P. The name comes from the Latin osculum, meaning “kiss.” It is the plane that comes closest to containing the part of the curve near P. （For a plane curve, the osculating plane is simply the plane that contains the curve.）

Kappa - Curvature of a Vector

Tangential & Normal Components of the Acceleration Vector of the Curve

When we study the motion of a particle, it is often useful to resolve the acceleration into two components, one in the direction of the tangent and the other in the direction of the normal.

Specifically

Vector Calculus

The Position Vector

（Original Function）

The Velocity Vector

（First Derivative）

The velocity vector is also the tangent vector and points in the direction of the tangent line.
The speed of the particle at time t is the magnitude of the velocity vector, that is,

The Acceleration Vector

（Second Derivative）

Matrices

Reference

The Determinant of A Matrix

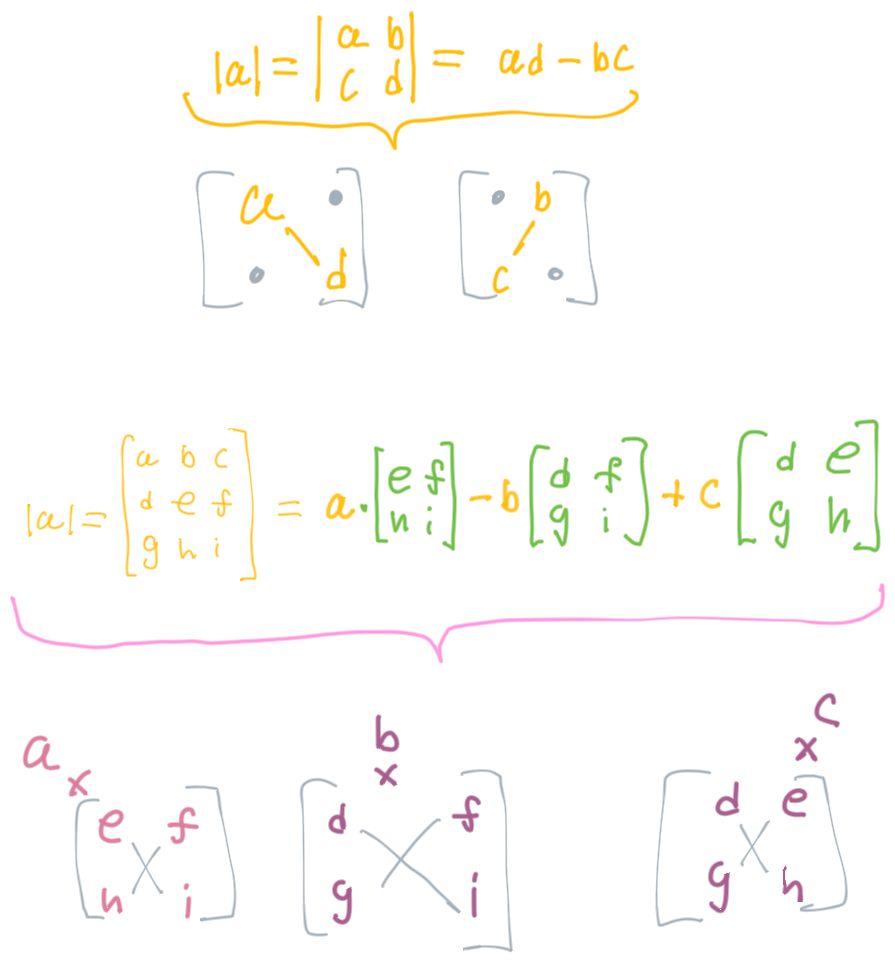
Only works for square matrices.

The Cross Product

Geometry

The Circle

Definition of a Line

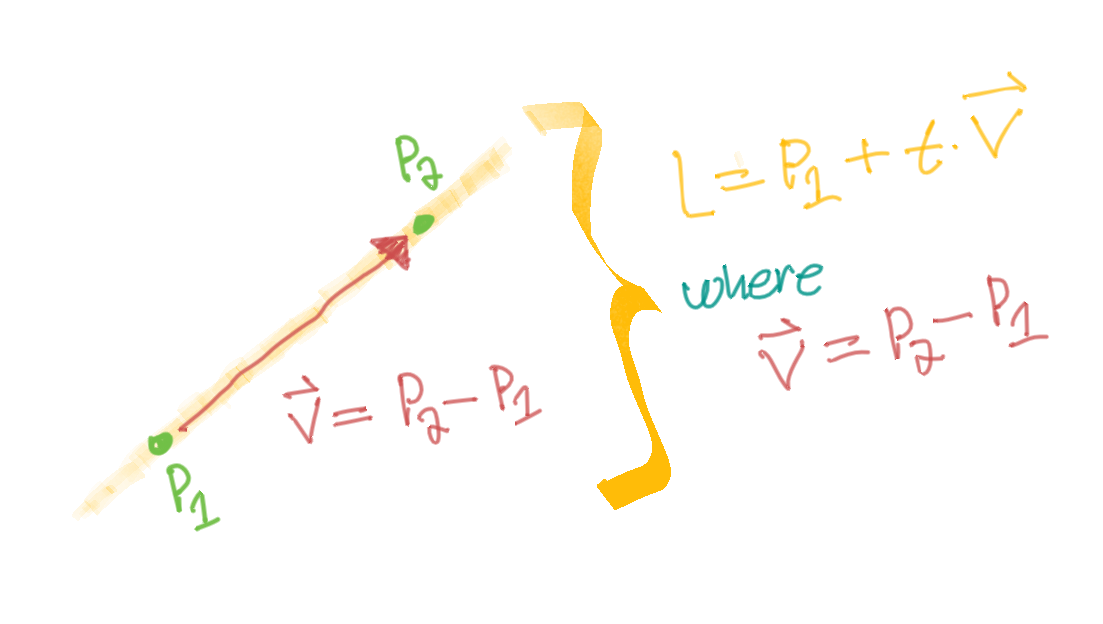
Vector Equation of a Line

Given

We can define a vector between and

Therefore

The equation of a line in 3D space or can be defined VIA the following options

That is

Parametric Equation of a Line

Essentially

That is, is the scaling factor. In a way, it's like it's a function of , but also similar to the slope （） in , except （i.e. ） is parameterized.

Sometimes this will be （confusingly） denoted as

Symmetric Equation of a Line

Therefore

Rationale

We rewrite in terms of .

That is

Parameterizations of a curve

Parametrized curve: A curve in the plane is said to be parameterized if the set of coordinates on the curve, （x,y）, are represented as functions of a variable t.; A parametrized Curve is a path in the xy-plane traced out by the point as the parameter ranges over an interval .; A parametrized Curve is a path in the xyz-plane traced out by the point as the parameter ranges over an interval .

Curvature Properties

Length of a Curve

The Arc Length Function

Suppose

Given some curve defined by some vector in
where is continuous and is traversed exactly once as increases from to

We can define it's arc length function VIA

If the limit is equal to zero; the test is inconclusive.

Geometric Series

Given

Alternatively

Tests

Furthermore

The Integral Test

Constraints on

Continuous
Positive
Decreasing （i.e. use derivative test）

If , this only means that the limit comparison test can be used. You still need to determine if either or converges or diverges.
Therefore, this does not apply to any arbitrary rational function.

Notes

For many series, we find a suitable comparison, , by keeping only the highest powers in the numerator and denominator of .

Exponential growth occurs when , and exponential decay occurs when .

The Law of Natural Growth:

The Logistic Model of Population Growth:

Where

If and are solutions; then is also a solution. Therefore, the most general solution to some second order homogeneous linear differential equations with constant coefficients would be .
This is why, when you find two solutions to the characteristic equation and respectively, we write it like so.

Given some:

We can presume that is of the form , and therefore:

Substituting this back into the original equation, we have:

Where:

So therefore:

Where the general solution is of the form:

Therefore

The above shows different ways of representing . （I.e. it doesn't correspond to some final solution.）

Arc Length

Formula for the arc length of a parametric curve over the interval .