Chapter 6 | Inverse Functions
§6.1 | Inverse Functions



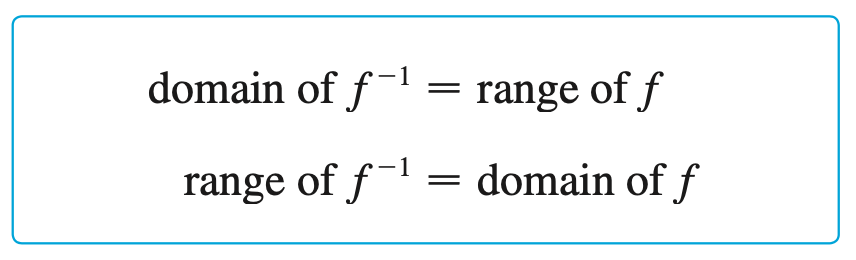
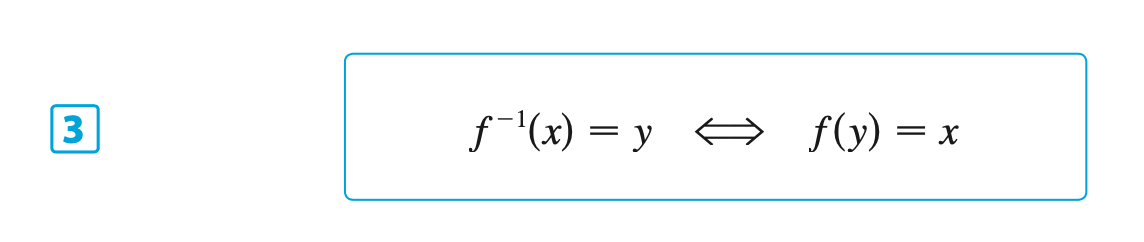
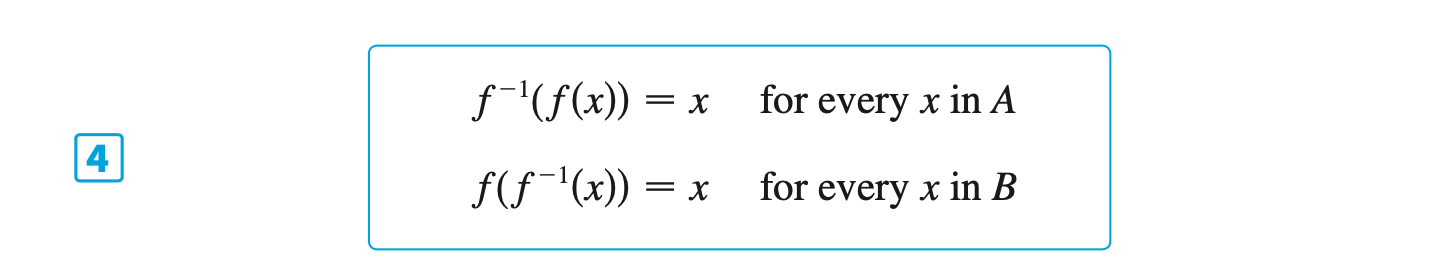




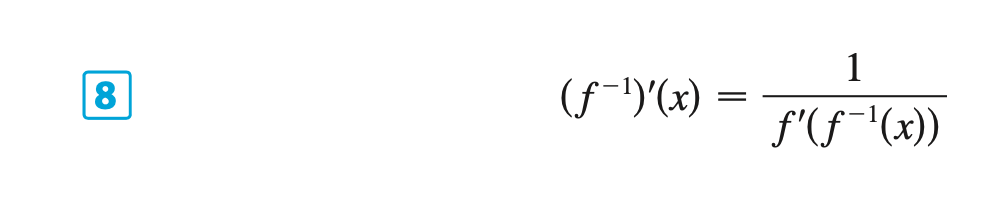
§6.2 | Exponential Functions and their Derivatives
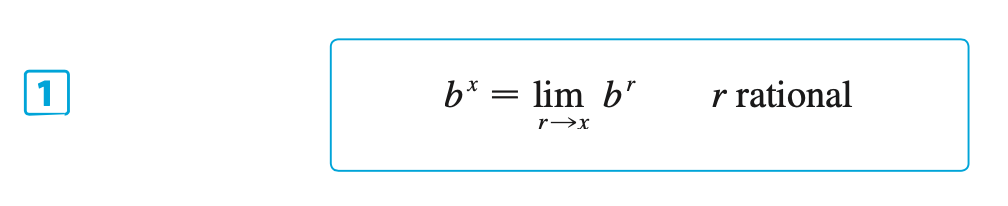

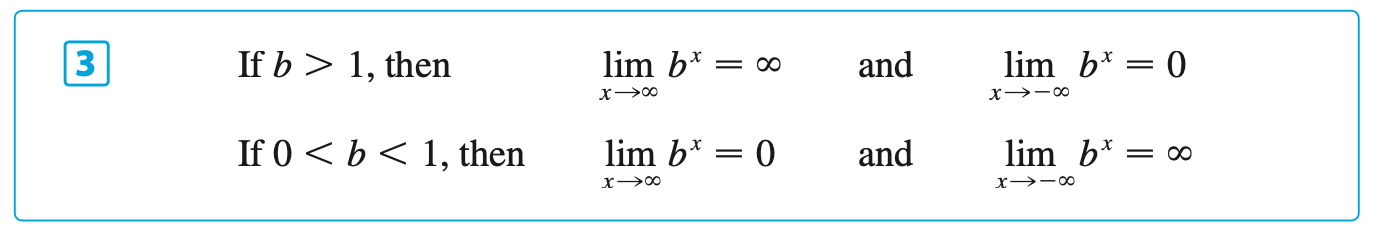

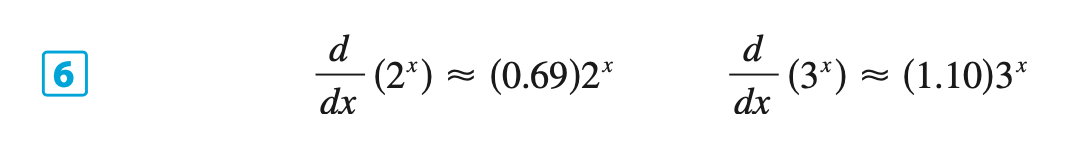


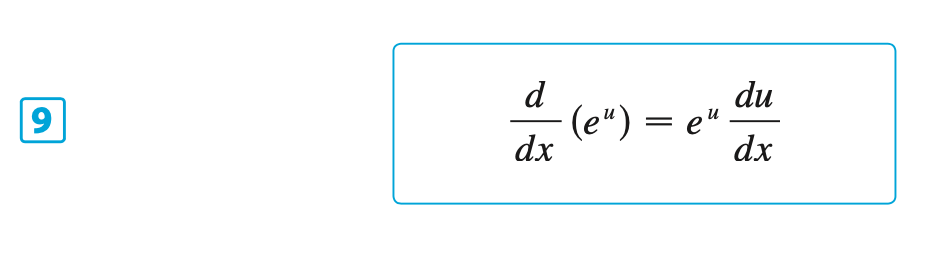

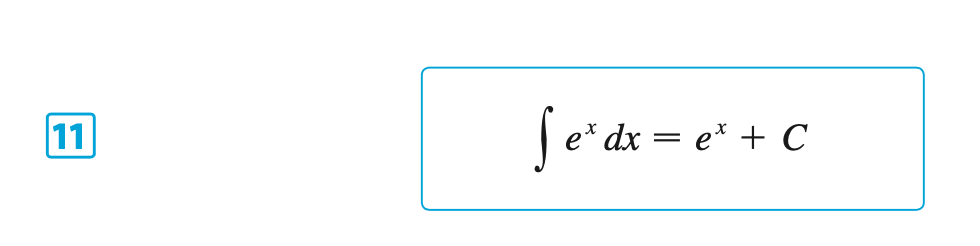
Other Formulas, Proofs & Facts for \(f(x) = b^x\)
Basic Exponential Formula
$$\begin{equation}
\begin{split}
f(x) &= a^x \\
f^{\prime}(x) &= a^x \cdot \ln(a) \\
\end{split}
\end{equation}$$
Generalized Exponential Formula
$$\begin{equation}
\begin{split}
f(x) &= a^{g(x)} \\
f^{\prime}(x)
&= a^{g(x)} \cdot \ln(a) \cdot \frac{\mathrm{d}}{\mathrm{d}x}\Big(g(x)\Big) \\\\
&= a^{g(x)} \cdot \ln(a) \cdot g^{\prime}(x) \\
\end{split}
\end{equation}$$
Exponential Formula Proof
$$
\newcommand{\d}[1]{\frac{\mathrm{d}}{\mathrm{d}{#1}}}
\newcommand{\df}[2]{\frac{\mathrm{d}{#1}}{\mathrm{d}{#2}}}
\begin{equation}
\begin{aligned}
\overbrace{f(x) = y = a^x}^{\text{apply $\ln$ to both sides}} \\
\ln y = \ln b^x \\
\overbrace{\ln y = x \cdot \ln a \\}^{\text{differentiate}} \\
\overbrace{\frac{1}{y} \df{y}{x} = \cdot 1 \ln a}^{\text{multiply both sides with $y$}} \\
\overbrace{\df{y}{x} = \ln a \cdot y}^{\text{plugin original $y$}} \\
\overbrace{\df{y}{x} = \ln a \cdot a^x}^{\text{answer}} \\\\
f^{\prime}(x) = \ln a \cdot a^x \\
\end{aligned}
\end{equation}
$$
Domain & Range
| Domain | Range |
| \((-\infty, \infty)\) | \((0, \infty)\) |
§6.3 | Logarithmic Functions
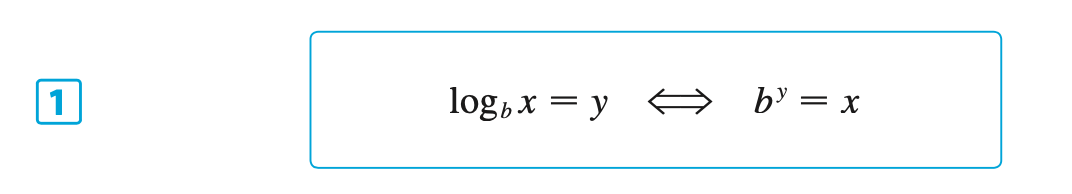
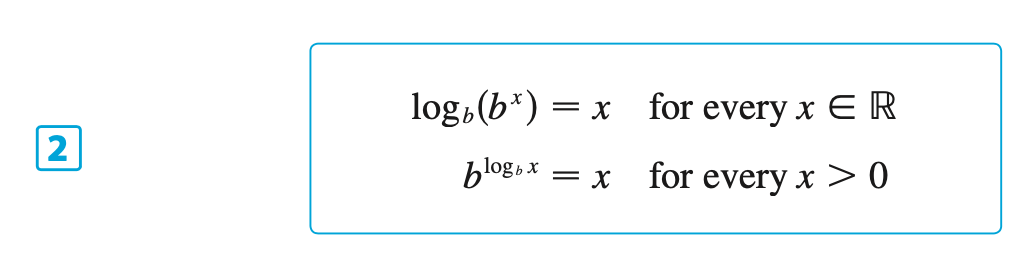


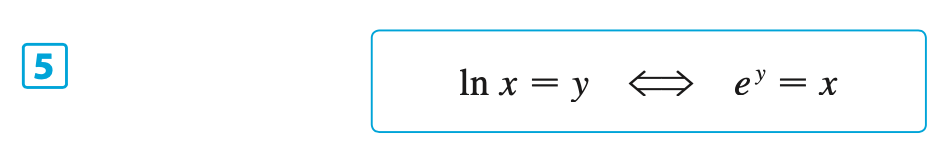
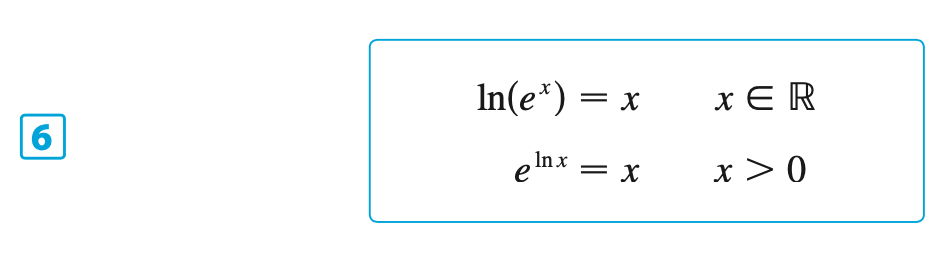
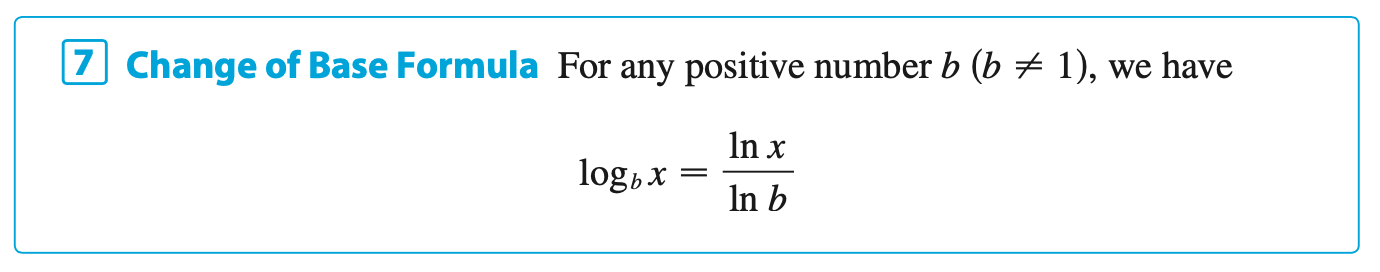
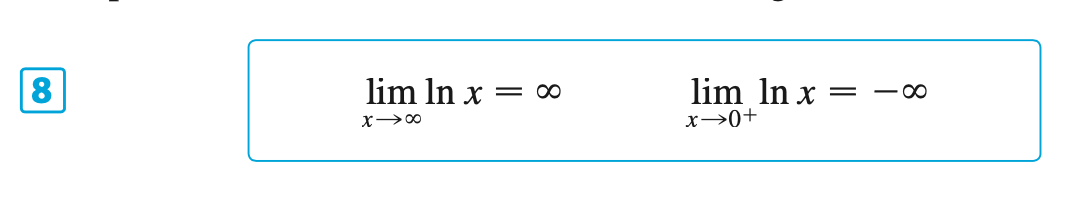
§6.4 | Derivatives of Logarithmic Functions
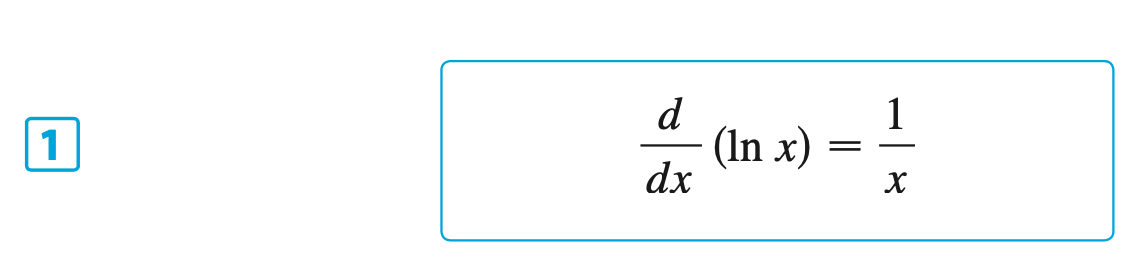

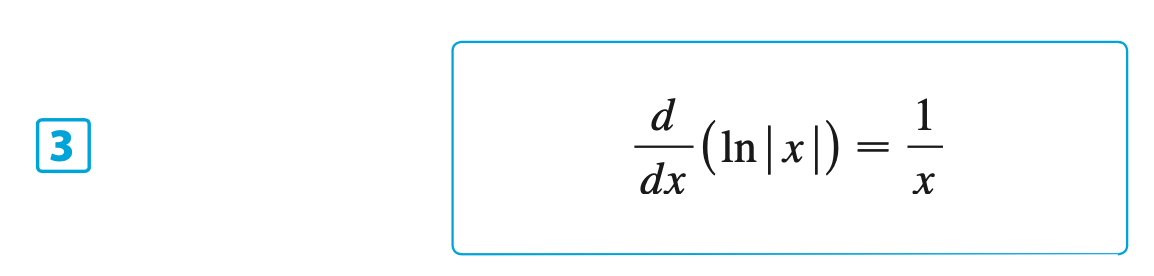
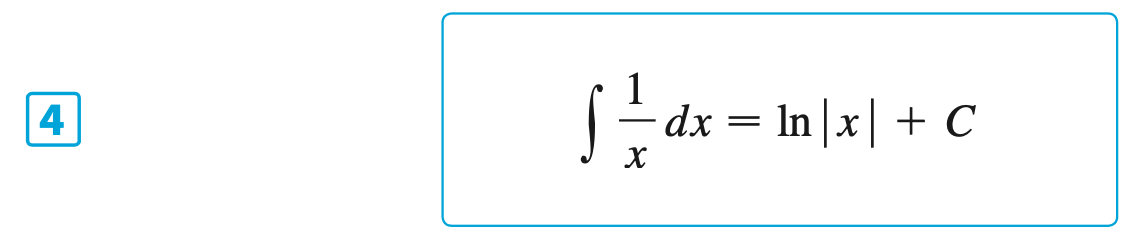


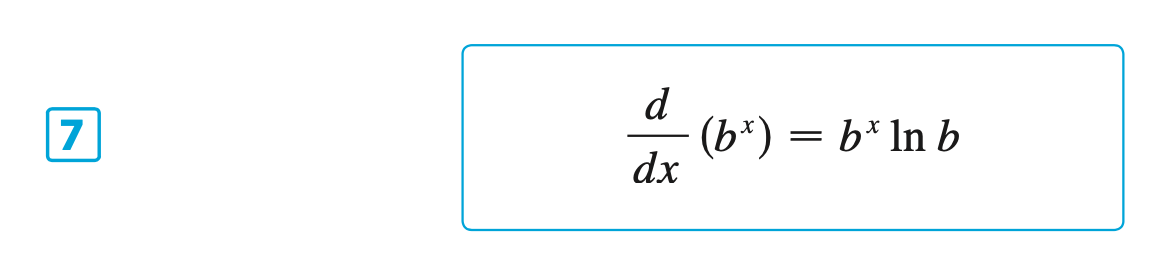
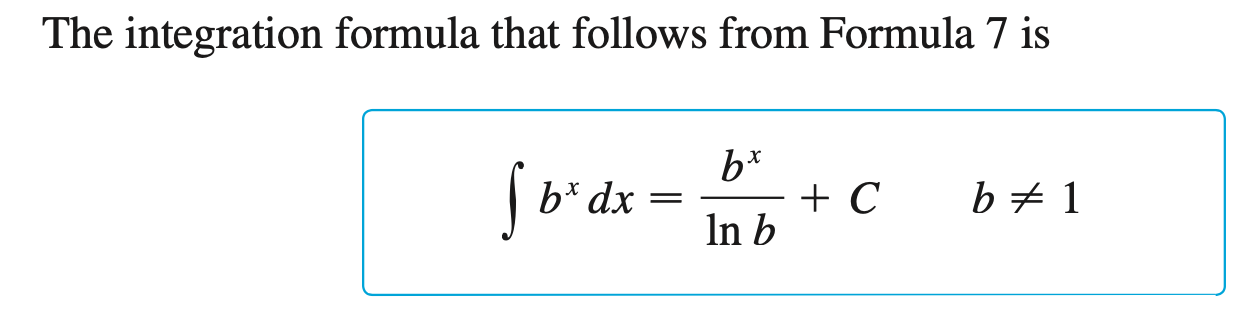

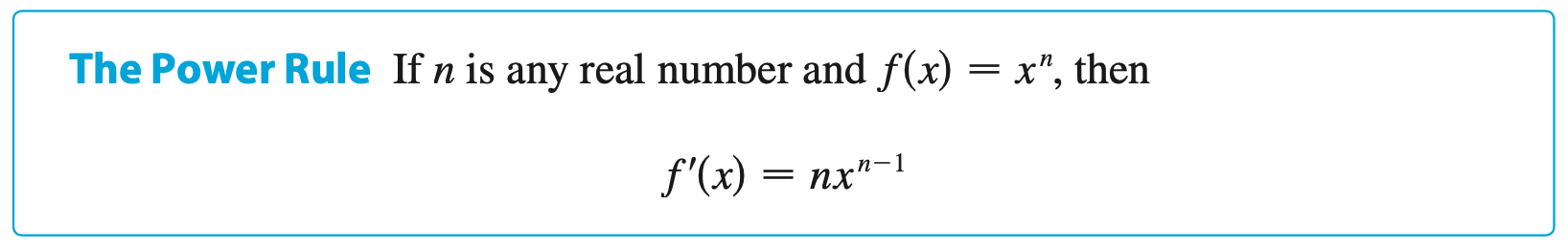
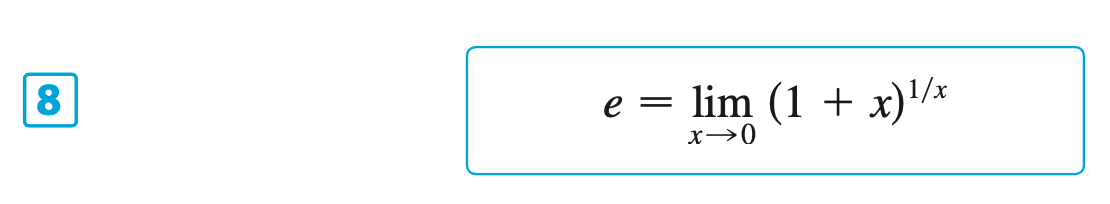
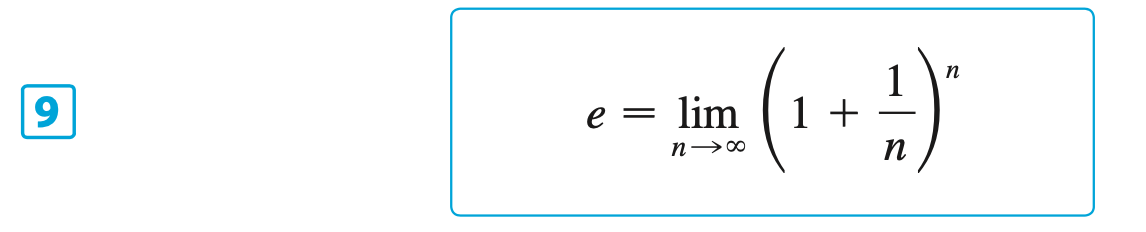
Other Formulas, Proofs & Facts for \(y = \log_b{x}\)
Basic Logarithmic Formula
$$\begin{equation}
\begin{split}
f(x) &= \log_{b}(x) \\\\
f^{\prime}(x) &= \frac{1}{x \cdot \ln(b)}
\end{split}
\end{equation}$$
Generalized Logarithmic Formula
$$\begin{equation}
\begin{split}
f(x) &= \log_{b}\left(g(x)\right) \\\\
f^{\prime}(x)
&= \frac{1}{g(x) \cdot \ln(b)} \cdot \frac{\mathrm{d}}{\mathrm{d}x}\Big(g(x)\Big) \\\\
&= \frac{1}{g(x) \cdot \ln(b)} \cdot g^{\prime}(x)
\end{split}
\end{equation}$$
Basic Exponential Formula
$$\begin{equation}
\begin{split}
f(x) &= a^x \\
f^{\prime}(x) &= a^x \cdot \ln(a) \\
\end{split}
\end{equation}$$
Generalized Exponential Formula
$$\begin{equation}
\begin{split}
f(x) &= a^{g(x)} \\
f^{\prime}(x)
&= a^{g(x)} \cdot \ln(a) \cdot \frac{\mathrm{d}}{\mathrm{d}x}\Big(g(x)\Big) \\\\
&= a^{g(x)} \cdot \ln(a) \cdot g^{\prime}(x) \\
\end{split}
\end{equation}$$
Exponential Formula Proof
$$
\newcommand{\d}[1]{\frac{\mathrm{d}}{\mathrm{d}{#1}}}
\newcommand{\df}[2]{\frac{\mathrm{d}{#1}}{\mathrm{d}{#2}}}
\begin{equation}
\begin{aligned}
\overbrace{f(x) = y = a^x}^{\text{apply $\ln$ to both sides}} \\
\ln y = \ln b^x \\
\overbrace{\ln y = x \cdot \ln a \\}^{\text{differentiate}} \\
\overbrace{\frac{1}{y} \df{y}{x} = \cdot 1 \ln a}^{\text{multiply both sides with $y$}} \\
\overbrace{\df{y}{x} = \ln a \cdot y}^{\text{plugin original $y$}} \\
\overbrace{\df{y}{x} = \ln a \cdot a^x}^{\text{answer}} \\\\
f^{\prime}(x) = \ln a \cdot a^x \\
\end{aligned}
\end{equation}
$$
Logarithmic Formula Proof
$$
\newcommand{\d}[1]{\frac{\mathrm{d}}{\mathrm{d}{#1}}}
\newcommand{\df}[2]{\frac{\mathrm{d}{#1}}{\mathrm{d}{#2}}}
\begin{equation}
\begin{split}
f(x) &= \log_{b}(x) \\\\
&= \overbrace{\frac{\ln(x)}{\ln(b)}}^{\text{change of base}} \\\\
&= \overbrace{\frac{1}{\ln(b)}}^{\text{constant}} \cdot \ln(x) \\\\
& \text{given}\\
& \d{x} \; \ln(x) = \frac{1}{x} \\\\
&\text{therefore} \\
f^{\prime}(x) &= \frac{1}{\ln(b)} \cdot \d{x}\Big(\ln(x) \Big) \\
&= \frac{1}{\ln(b)} \cdot \frac{1}{x} \\
&= \frac{1}{x \cdot \ln b}
\end{split}
\end{equation}
$$
Change of Base Formula
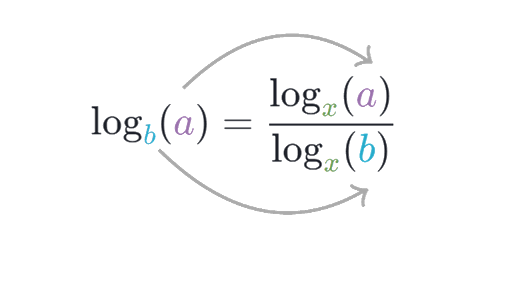
Domain & Range
| Domain | Range |
| \((0, \infty)\) | \((-\infty, \infty)\) |
§6.5 | Exponential Growth and Decay
§6.6 | Inverse Trigonometric Functions
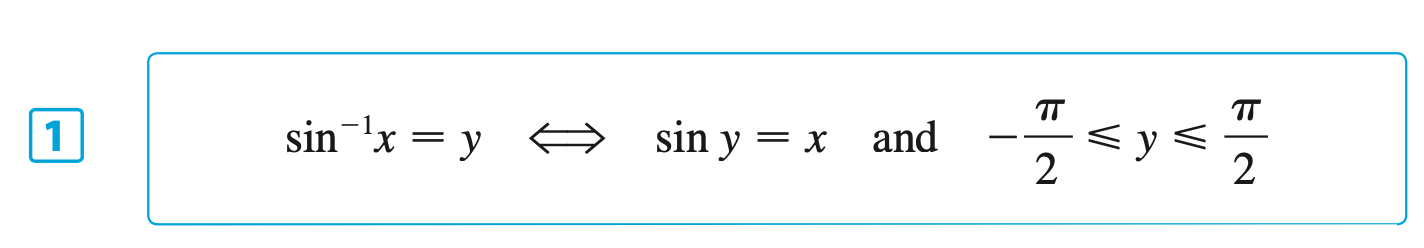
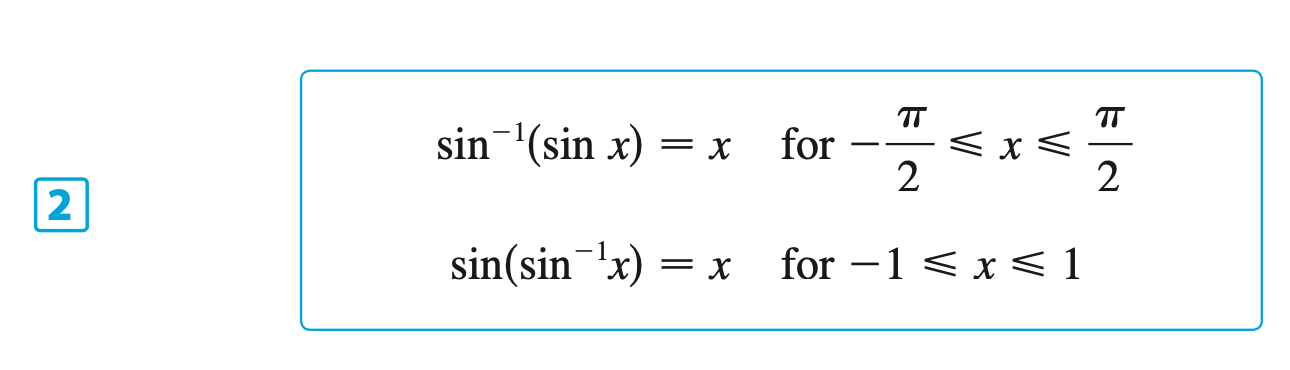
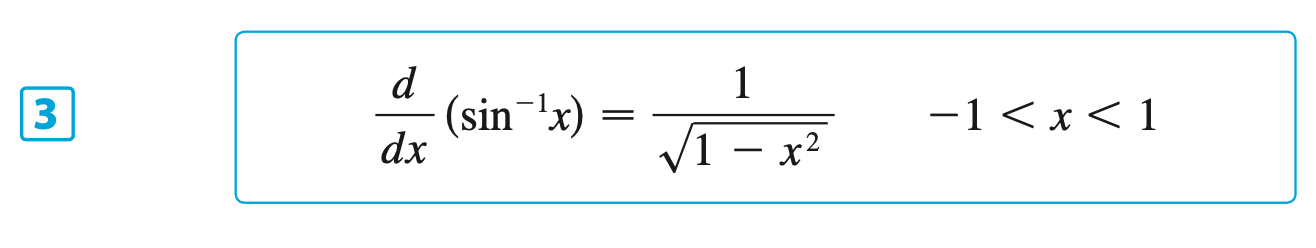

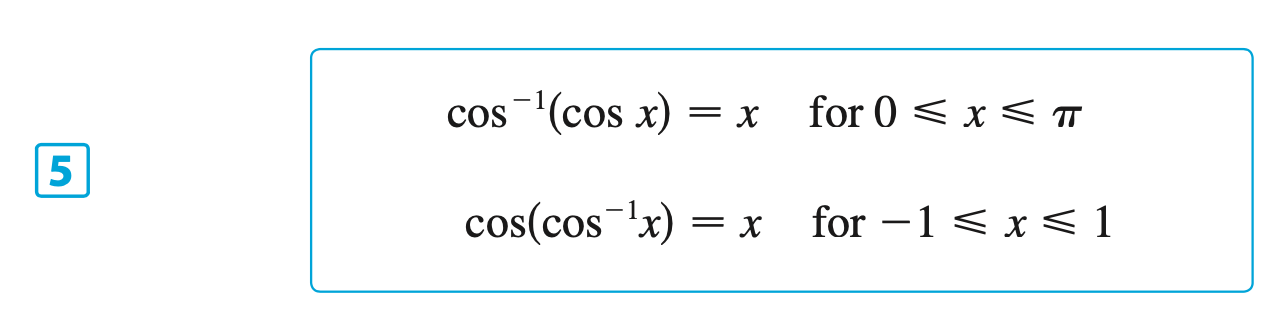
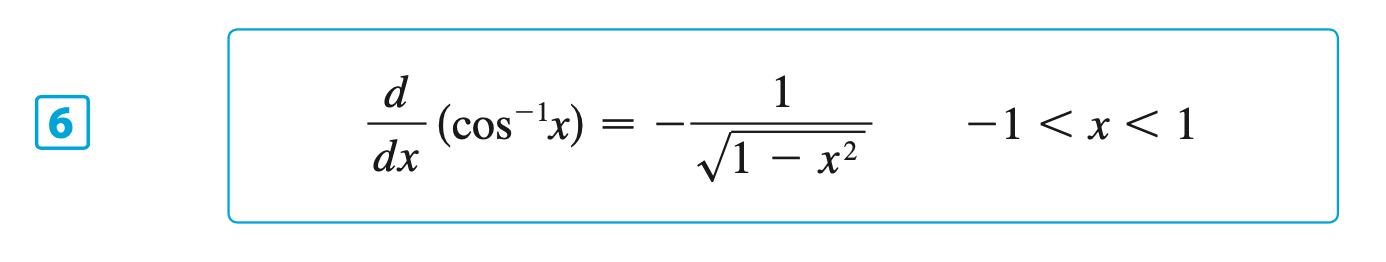
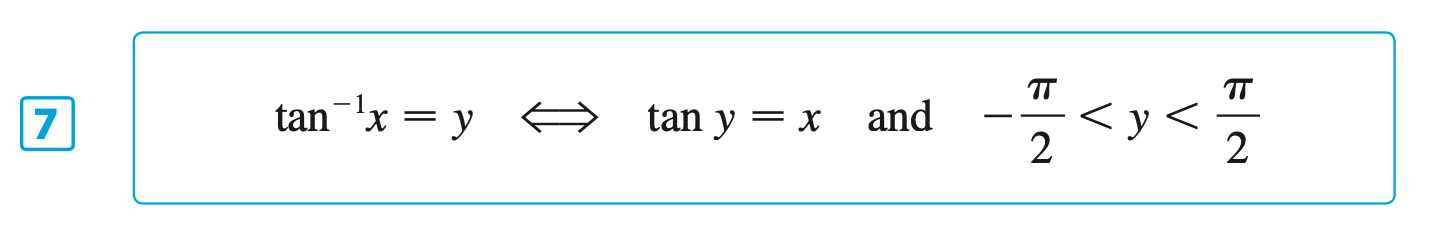
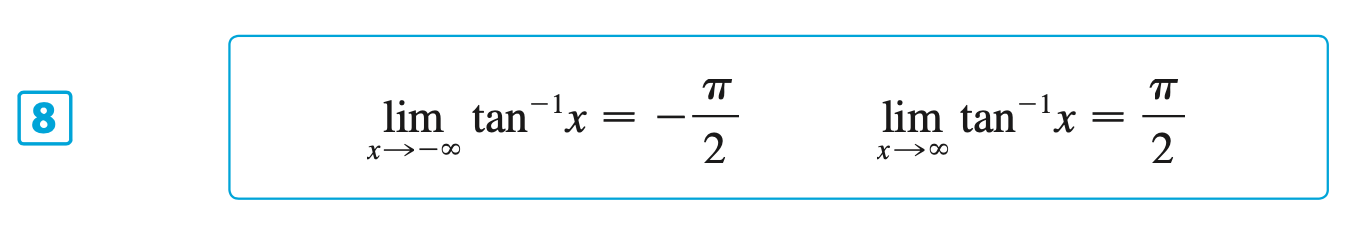
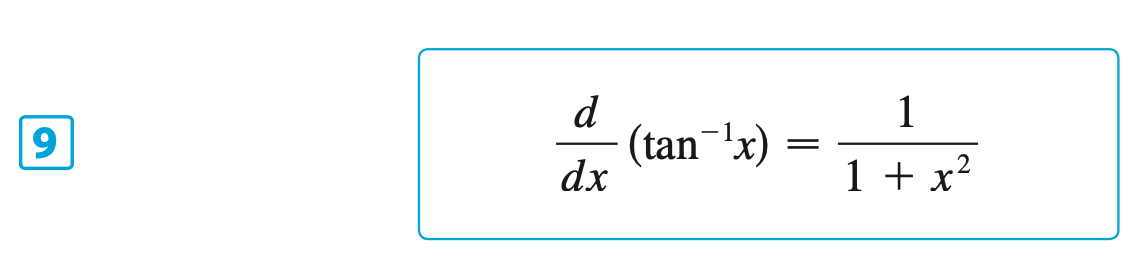
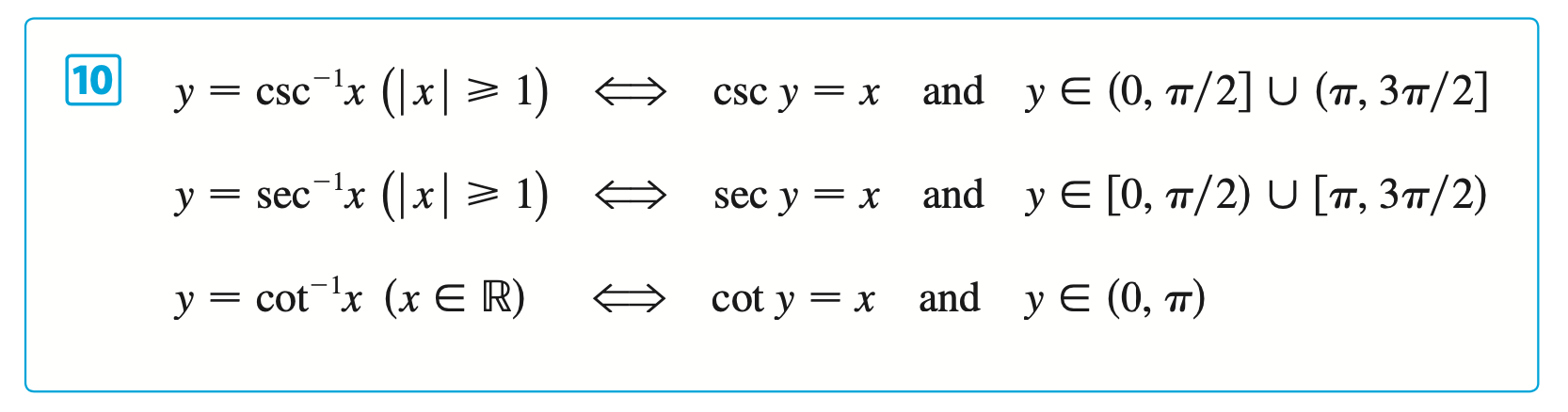

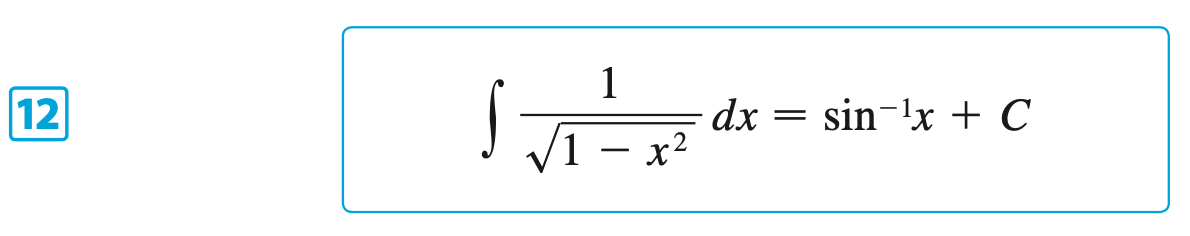
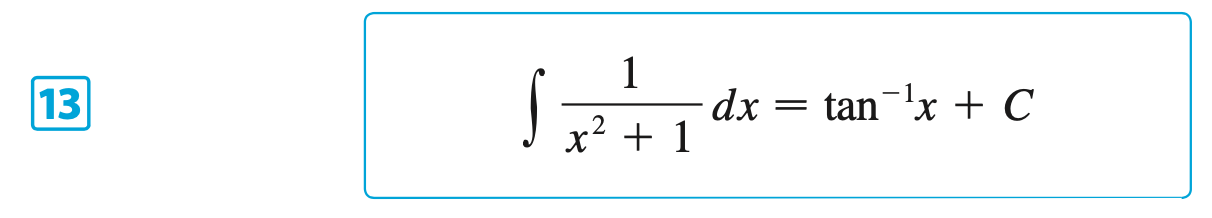
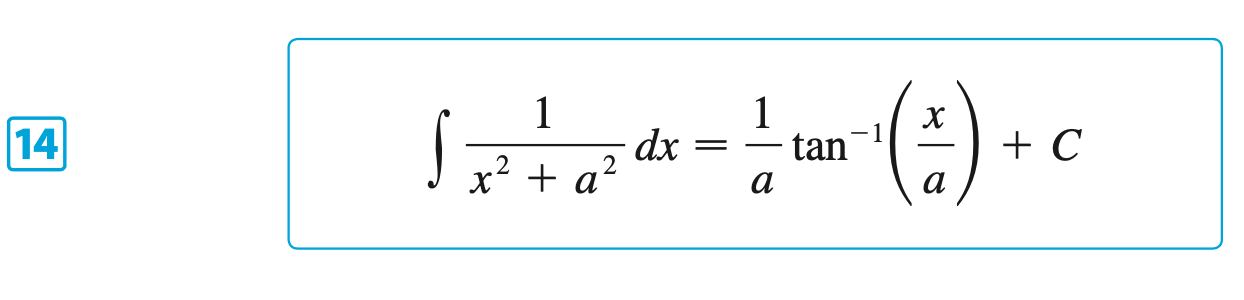
§6.7 | Hyperbolic Functions
§6.8 | Indeterminate Forms and the L'Hopital's Rule




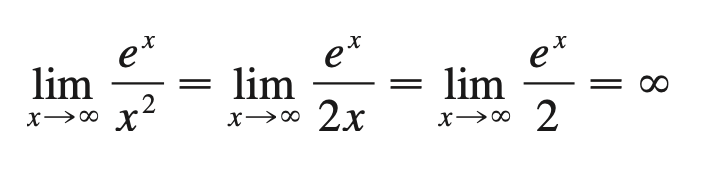
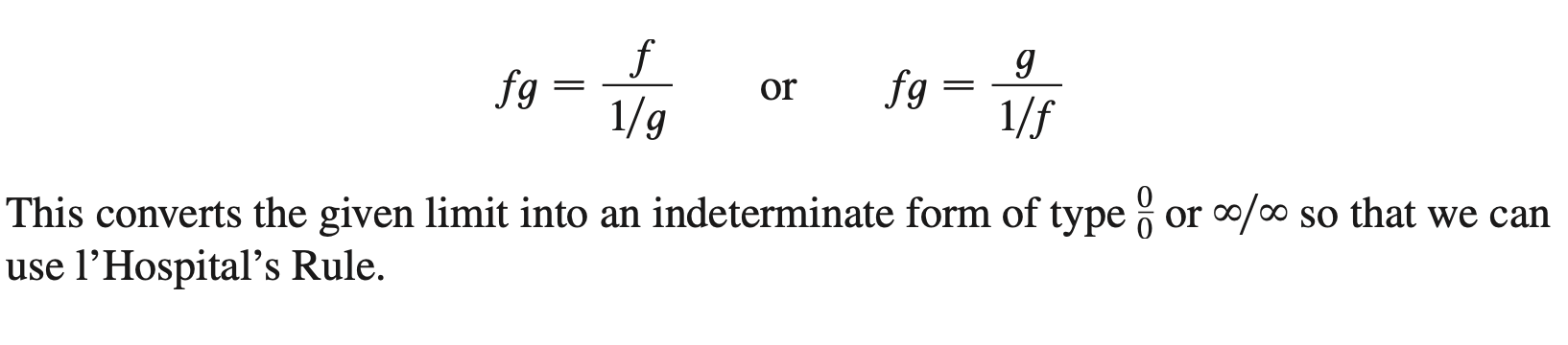




§6 | Miscellaneous
Review
#5
$$
e^{2\ln(3)} = 3^2 = 9
$$
#6A
Begin
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\underbrace{
\begin{aligned}
\ln(1 + e^{-x}) &= 3 \\
e^3 &= 1 + e^{-x} \\
e^3 - 1 &= e^{-x}
\end{aligned}
}_{\text{Apply $\ln$ to both sides}}
\end{equation}
$$
$$
\begin{equation}
\begin{split}
\ln \left(e^3 - 1\right) &= \ln\left(e^{-x}\right) \\
\ln \left(e^3 - 1\right) &= -x \cdot \ln\left(e\right) \\
\ln \left(e^3 - 1\right) &= -x \cdot (1) \\
\ln \left(e^3 - 1\right) &= -x \\
-\ln \left(e^3 - 1\right) &= x
\end{split}
\end{equation}
$$
Answer
$$
\begin{equation}
x = -\ln \left(e^3 - 1\right)
\end{equation}
$$
#6B
Begin
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\underbrace{
\begin{aligned}
\lnp{x + 1} + \lnp{x - 1} &= 1 \\
\lnp{(x + 1)(x - 1)} &= 1 \\
\lnp{x^2 - 1} &= 1 \\
e^1 &= x^2 - 1 \\
1 + e^1 &= x^2 \\
\sqrt{1 + e^1} &= \sqrt{x^2} \\
\pm \sqrt{1 + e^1} &= x \\
\sqrt{1 + e^1} &= x \\
\end{aligned}
}_{\text{no $\pm$ because of domain}}
\end{equation}
$$
Answer
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
x = \sqrt{1 + e^1}
\end{equation}
$$
#6C
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\begin{split}
tan^{-1}(x) &= 1 \\
x &= \frac{1}{8}\tau = \frac{1}{4}\pi
\end{split}
\end{equation}
$$
#6D
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\begin{split}
\sin(x) &= 0.3 = \frac{3}{10} \\
x = \arcsin(\frac{3}{10})
\end{split}
\end{equation}
$$
#7A
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\begin{split}
f(x) = y &= \ln |\sec(5x) + \tan(5x)| \\\\
f^\prime(x)
&= \frac{1}{\sec(5x) + \tan(5x)} \cdot \Big(\sec(5x) + \tan(5x)\Big)^{\prime} \\\\
&= \frac{\frac{5\sin(5x)}{\cos^2(x)} + 5\sec^2(5x)}{\sec(5x) + \tan(5x)}
\end{split}
\end{equation}
$$
Since
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\begin{split}
\dox \sec(5x)
&= \dox \frac{1}{\cos(5x)} \\
&= \dox \frac{A}{B} \\
&= \frac{A^{\prime} B - A B^{\prime}}{B^2} \\
&= \frac{0\cos(5x) - (-5\sin(5x))}{\cos^2(x)} \\
&= \frac{5\sin(5x)}{\cos^2(x)} \\
\dox \tan(5x) &= 5\sec^2(5x)
\end{split}
\end{equation}
$$
Answer
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
f^\prime(x) = \frac{\frac{5\sin(5x)}{\cos^2(x)} + 5\sec^2(5x)}{\sec(5x) + \tan(5x)}
\end{equation}
$$
#7B
Begin
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\begin{split}
f(x) = y
&= x \cdot \tan^{-1}(4x) \\
&= A \cdot B \\
f^{\prime}(x)
&= A^{\prime} B + A B^{\prime} \\
&= \tan^{-1}(4x) + x \frac{1}{1 + (4x)^2} \cdot \dox\Big(4x\Big) \\
&= \tan^{-1}(4x) + \frac{4x}{1 + 16x^2}
\end{split}
\end{equation}
$$
Answer
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
f^\prime(x) = \tan^{-1}(4x) + \frac{4x}{1 + 16x^2}
\end{equation}
$$
#7C
Begin
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\begin{split}
f(x) = y
&= e^{mx} \cdot \cos(n x) \\
&= AB \\
f^{\prime}(x)
&= \dox AB \\
&= A^{\prime} B + A B^{\prime} \\
&= \left(m e^{mx}\right) \cos(n x) + e^{mx} -\sin(n x) \cdot \dox\Big(n x\Big) \\
&= m e^{mx}\cos(n x) - n e^{mx}\sin(n x)
\end{split}
\end{equation}
$$
Answer
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
f^\prime(x) = m e^{mx}\cos(n x) - n e^{mx}\sin(n x)
\end{equation}
$$
#7D
Begin
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\begin{split}
f(x) = y &= 3^{x \cdot \ln(x)} \\
f^\prime(x)
&= 3^{x \cdot \ln(x)} \cdot \ln(3) \cdot \dox\Big(x \cdot \ln(x)\Big) \\
&= 3^{x \cdot \ln(x)} \cdot \ln(3) \cdot \Big(\ln(x) + 1\Big) \\
&= \ln(3) \cdot 3^{x \cdot \ln(x)} \cdot \Big(\ln(x) + 1\Big)
\end{split}
\end{equation}
$$
Where
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\begin{split}
\dox\Big(x \cdot \ln(x)\Big)
&= \cdot AB \\
&= A^{\prime} B + A B^{\prime} \\
&= \ln(x) + x \frac{1}{x} \\
&= \ln(x) + 1 \\
\end{split}
\end{equation}
$$
Answer
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
f^\prime(x) = \ln(3) \cdot 3^{x \cdot \ln(x)} \cdot \Big(\ln(x) + 1\Big)
\end{equation}
$$
#19A
Given
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\lim_{x \to \infty} e^{-3x} = \lim_{x \to \infty} e^{u}
\end{equation}
$$
Let
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
u = -3x
\end{equation}
$$
As
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
x \to \infty, \;\; u \to -\infty
\end{equation}
$$
Therefore
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\lim_{x \to \infty} e^{-3x} = \lim_{u \to -\infty} e^u = 0
\end{equation}
$$
Using the definition from the textbook
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\lim_{x \to -\infty} e^x = 0
\end{equation}
$$
#19B
Given
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\lim_{x \to 10^{-}} \ln(100 - x^2)
\end{equation}
$$
Let
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
u = 100 - x^2
\end{equation}
$$
As
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
x \to 10, \;\; u \to 0
\end{equation}
$$
Therefore
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\lim_{x \to 10^{-}} \ln(100 - x^2) = \lim_{u \to 0} \ln(u) = -\infty
\end{equation}
$$
Using the definition from the textbook
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\lim_{x \to 0} \ln(x) = -\infty
\end{equation}
$$
#19C
Given
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\lim_{x \to \infty} \arctan(x^3 - x)
\end{equation}
$$
Let
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\underbrace{u = x^3 - x = x(x^2 - 1) = x(x + 1)(x - 1)}_{\text{Odd - Increasing Function}}
\end{equation}
$$
As
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
x \to \infty, \;\; u \to \infty
\end{equation}
$$
Therefore
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\lim_{x \to \infty} \arctan(x^3 - x) = \lim_{u \to \infty} \arctan(u) = \frac{\pi}{2}
\end{equation}
$$
Using the definition from the textbook
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\lim_{x \to \infty} \arctan(x) = \frac{\pi}{2}
\end{equation}
$$
#19D
Begin:
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\newcommand{\eqWithMsg}[1]{\overset{{#1}}{=}}
\begin{equation}
\begin{split}
\lim_{x \to 0} \frac{e^{4x} - 1 - 4x}{x^2}
&\eqWithMsg{\frac{0}{0}} \lim_{x \to 0} \frac{4e^{4x} - 4}{2x} \\\\
&\eqWithMsg{\frac{0}{0}} \lim_{x \to 0} \frac{16e^{4x}}{2} \\\\
&= \frac{16}{2} \lim_{x \to 0} e^{4x} \\\\
&= 8 \lim_{x \to 0} e^{4x} \\\\
\end{split}
\end{equation}
$$
Let
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
u = 4x
\end{equation}
$$
As
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
x \to 0, \;\; u \to 0
\end{equation}
$$
Therefore
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\newcommand{\eqWithMsg}[1]{\overset{{#1}}{=}}
\begin{equation}
\begin{split}
\lim_{x \to 0} e^{4x} &= \lim_{u \to 0} e^u \eqWithMsg{DSP} e^0 = 1 \\\\
8\lim_{x \to 0} e^{4x} &= 8\lim_{u \to 0} e^u = 8(1) = 8
\end{split}
\end{equation}
$$
#19E
Begin
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\begin{split}
\lim_{x \to \infty} \frac{e^{4x} - 1 - 4x}{x^2}
&\eqWithMsg{\frac{0}{0}} \lim_{x \to \infty} \frac{4e^{4x} - 4}{2x} \\\\
&\eqWithMsg{\frac{0}{0}} \lim_{x \to \infty} \frac{16e^{4x}}{2} \\\\
&= \frac{16}{2} \lim_{x \to \infty} e^{4x} \\\\
&= 8 \lim_{x \to \infty} e^{4x} \\\\
\end{split}
\end{equation}
$$
Let
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
u = 4x
\end{equation}
$$
As
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
x \to \infty, \;\; u \to \infty
\end{equation}
$$
Therefore
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\begin{split}
\lim_{x \to 0} e^{4x} &= \lim_{u \to 0} e^u = \infty \\\\
8\lim_{x \to 0} e^{4x} &= 8\lim_{u \to 0} e^u = 8 \cdot \infty = \infty
\end{split}
\end{equation}
$$
Using the definition from the textbook
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\lim_{x \to \infty} e^x = \infty
\end{equation}
$$
#19F
Begin
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\begin{split}
\lim_{x \to -\infty} \Big( x^2 - x^3 \Big) e^{2x}
\end{split}
\end{equation}
$$
Let
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\begin{split}
u &= \overbrace{x^2 - x^3 = x^2(1 - x)}^{\text{Odd, Decreasing Function}} \\
v &= 2x \\
\end{split}
\end{equation}
$$
As
$$
\newcommand{\dox}{\frac{\mathrm{d}}{\mathrm{d}x}}
\newcommand{\lnp}[1]{\ln\left({#1}\right)}
\begin{equation}
\begin{split}
x \to -\infty, \;\; u \to \infty \\
x \to -\infty, \;\; v \to -\infty \\
\end{split}
\end{equation}
$$
TODO: L'Hopital's Rule