$$V = A \cdot h$$

Solids of revolution

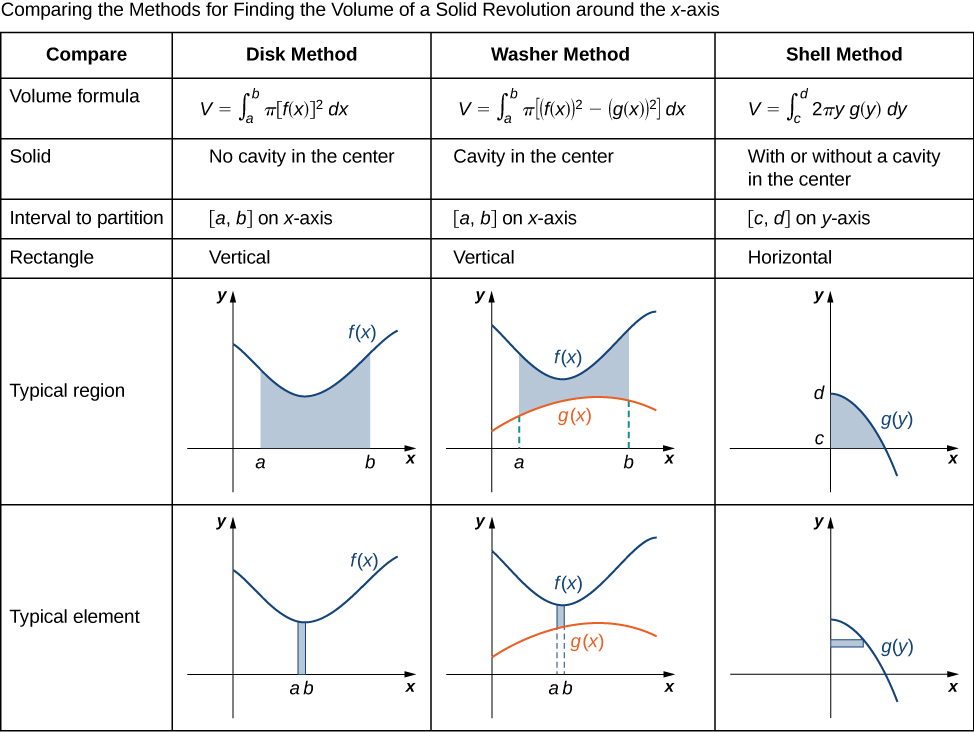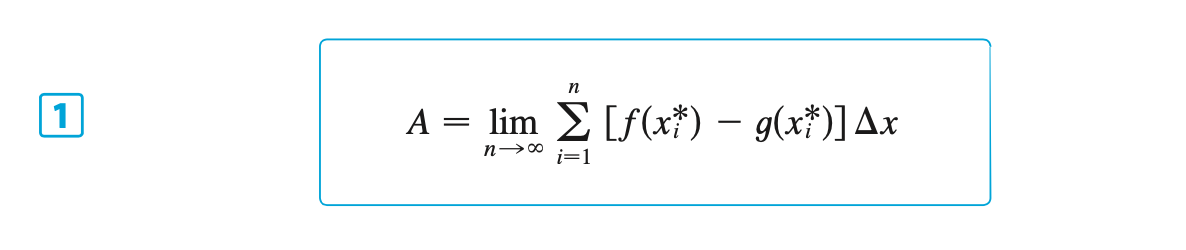
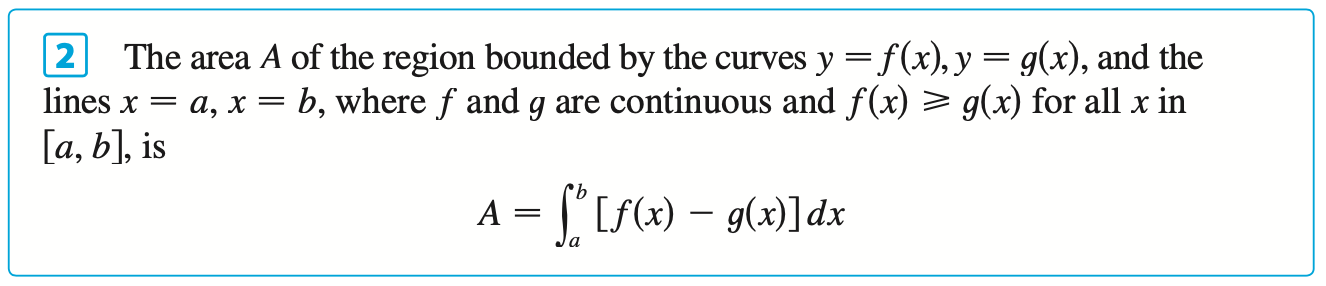
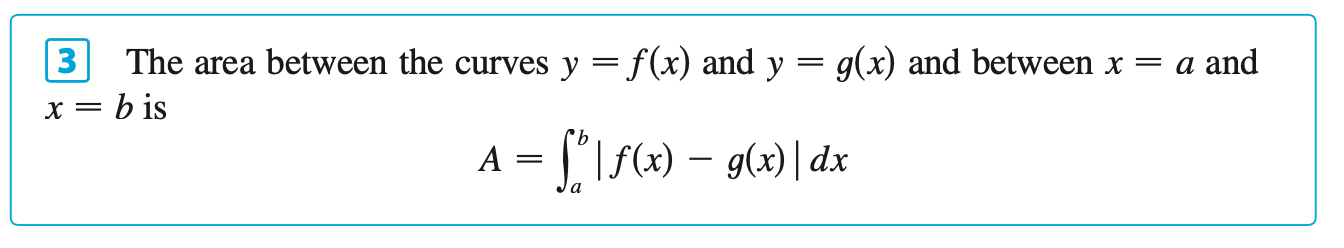
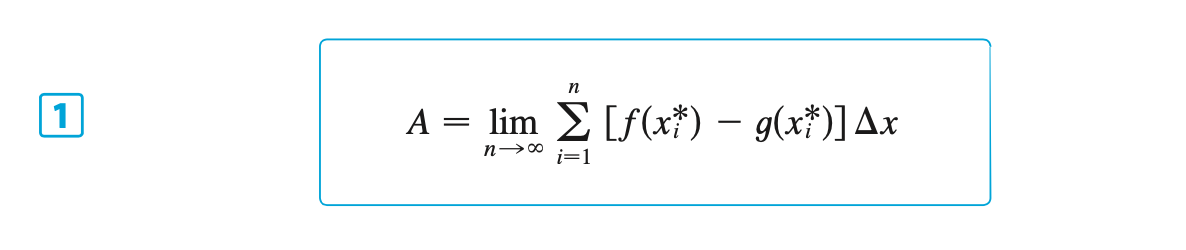
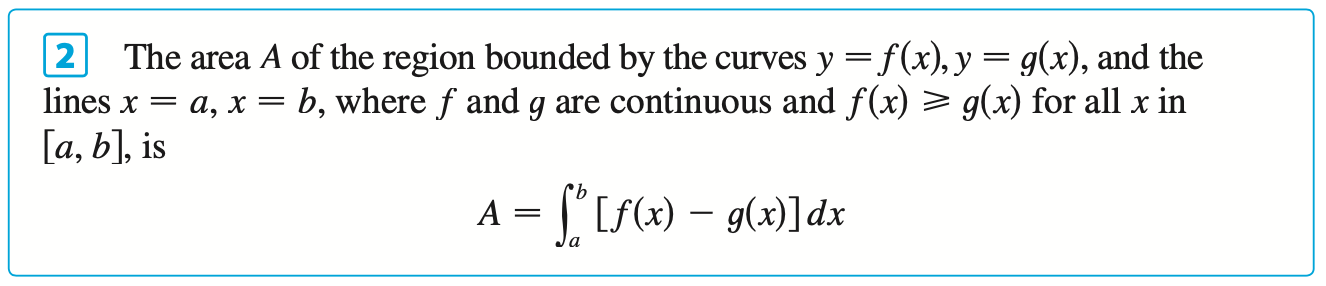
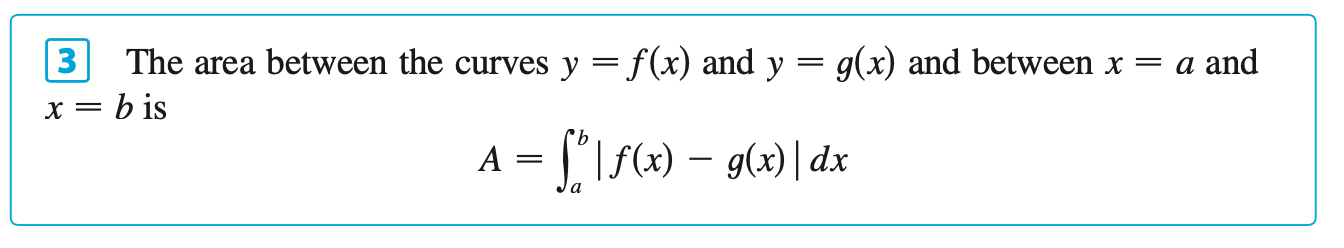
Called Solids of revolution because they are obtained by revolving a region about a line. In general, we calculate the volume of a solid of revolution by using the basic defining formula

$$V=\IntegrateFor{a}{b}{A(x)}{x}$$

$$V=\IntegrateFor{c}{d}{A(y)}{y}$$

Cross-sectional Area

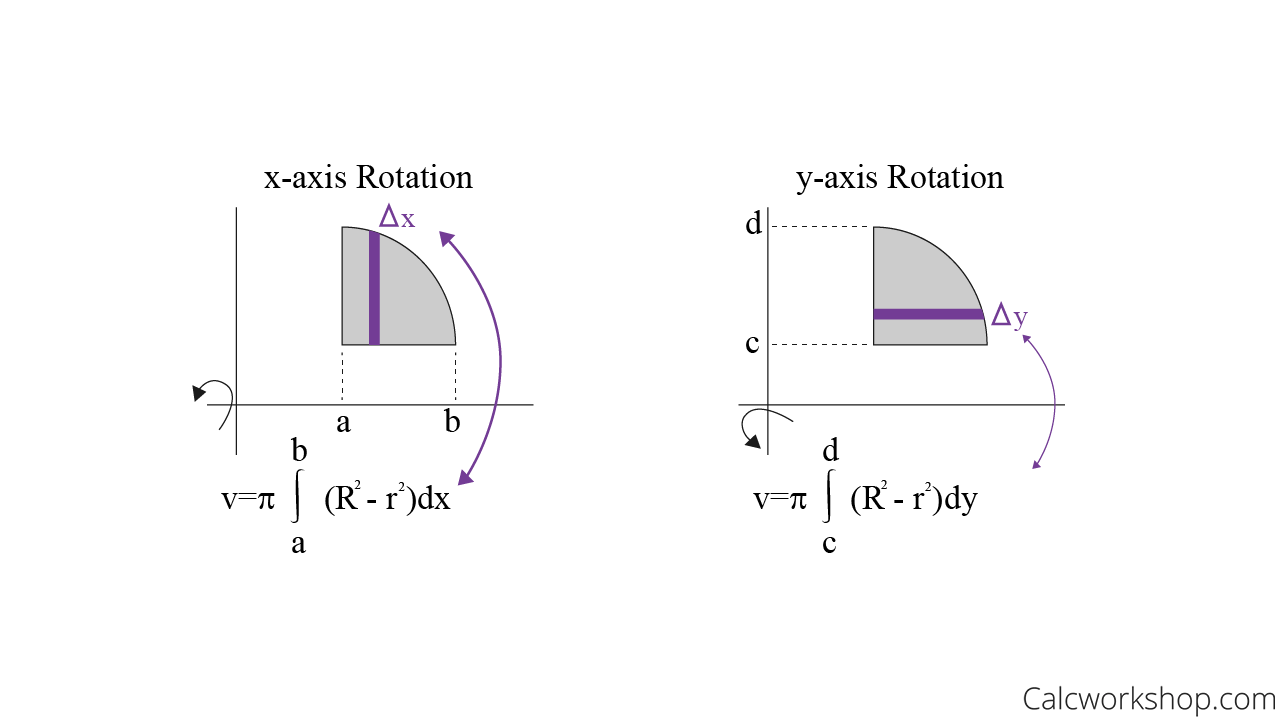
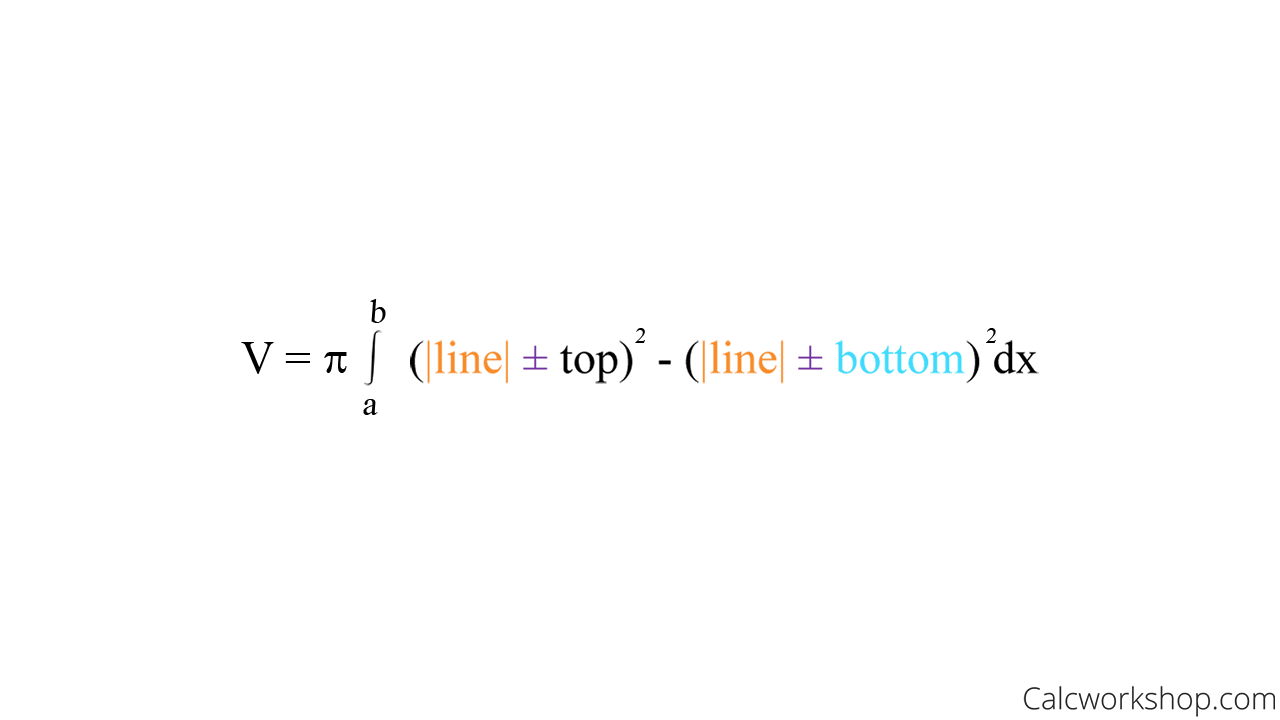
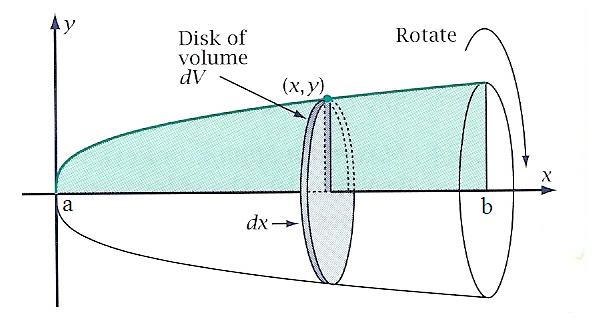
We find the cross-sectional area $A(x)$ or $A(y)$ in one of the following ways:

If the cross-section is a disk (i.e. a solid shape), we find the radius of the disk (in terms of x or y) and use
$$A = \pi\left(\text{radius}\right)^2$$

Disk Function Examples
If the cross-section is a washer (i.e. a hollow shape), we find the inner radius $r_{\text{in}}$ and outer radius $r_{\text{out}}$ from a sketch and compute the area of the washer by subtracting the area of the inner disk from the area of the outer disk:
$$A = \pi\left(\text{outer radius}\right)^2 - \pi\left(\text{inner radius}\right)^2$$

Washer Function Examples

The Shell Method

Significant Distinction

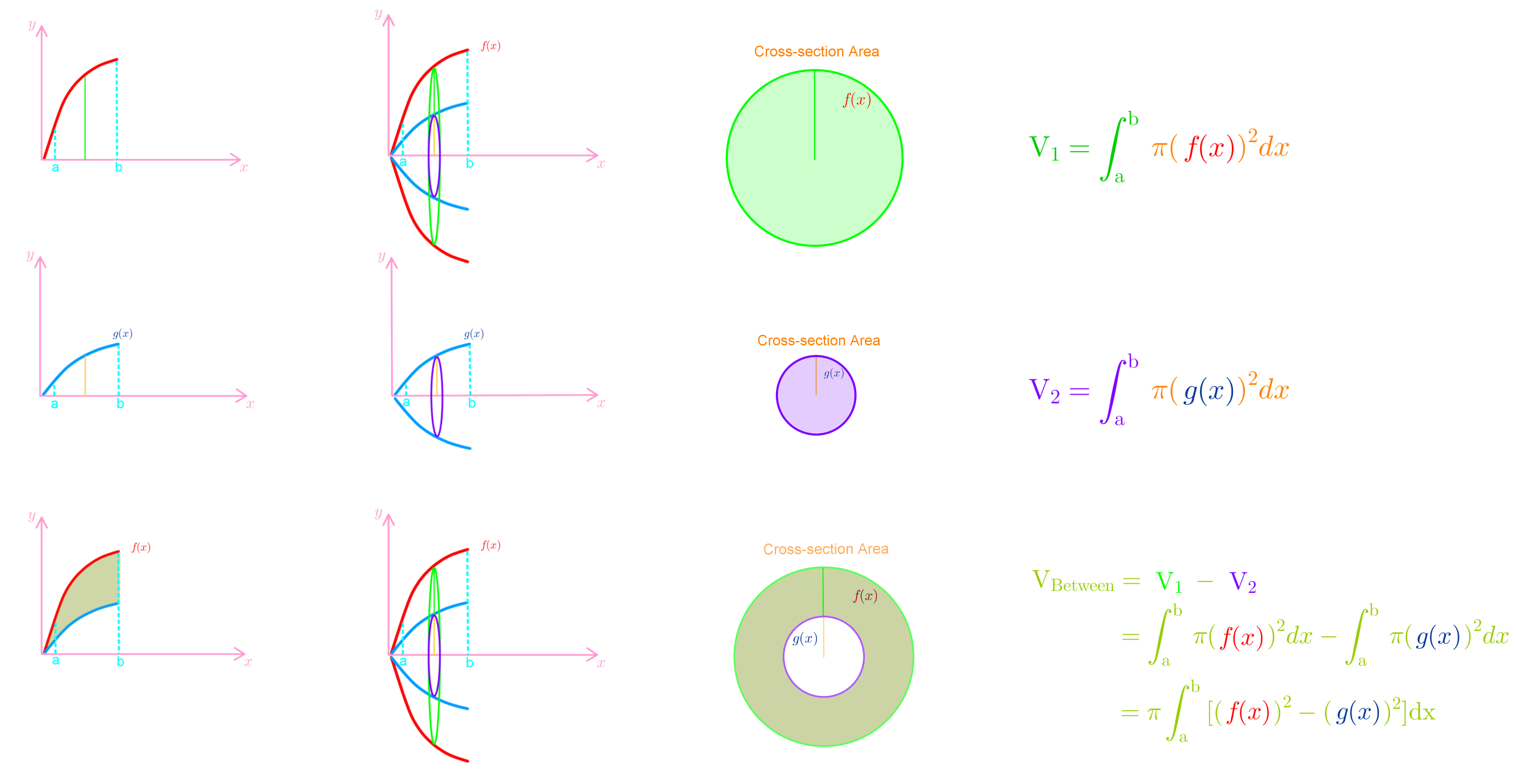
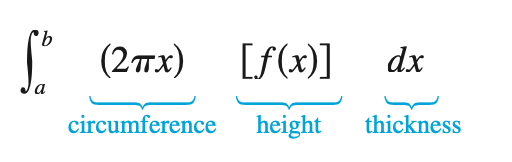
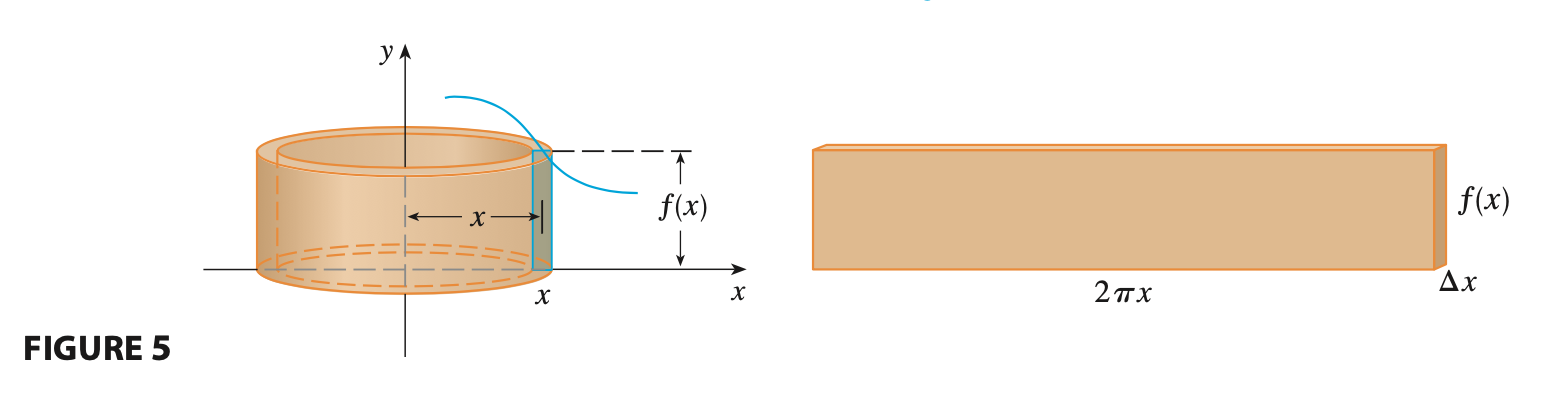
For the disk/washer method, the slice is perpendicular to the axis of revolution, whereas, for the shell method, the slice is parallel to the axis of revolution.

Alternatively

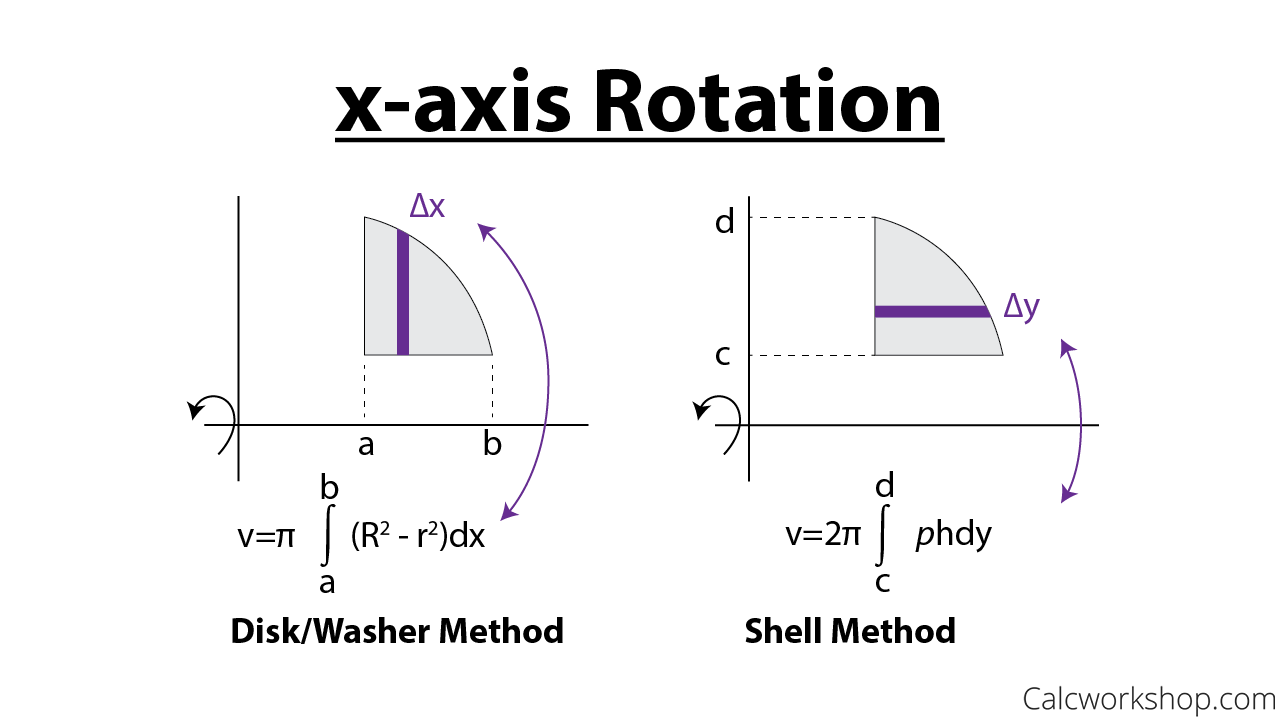
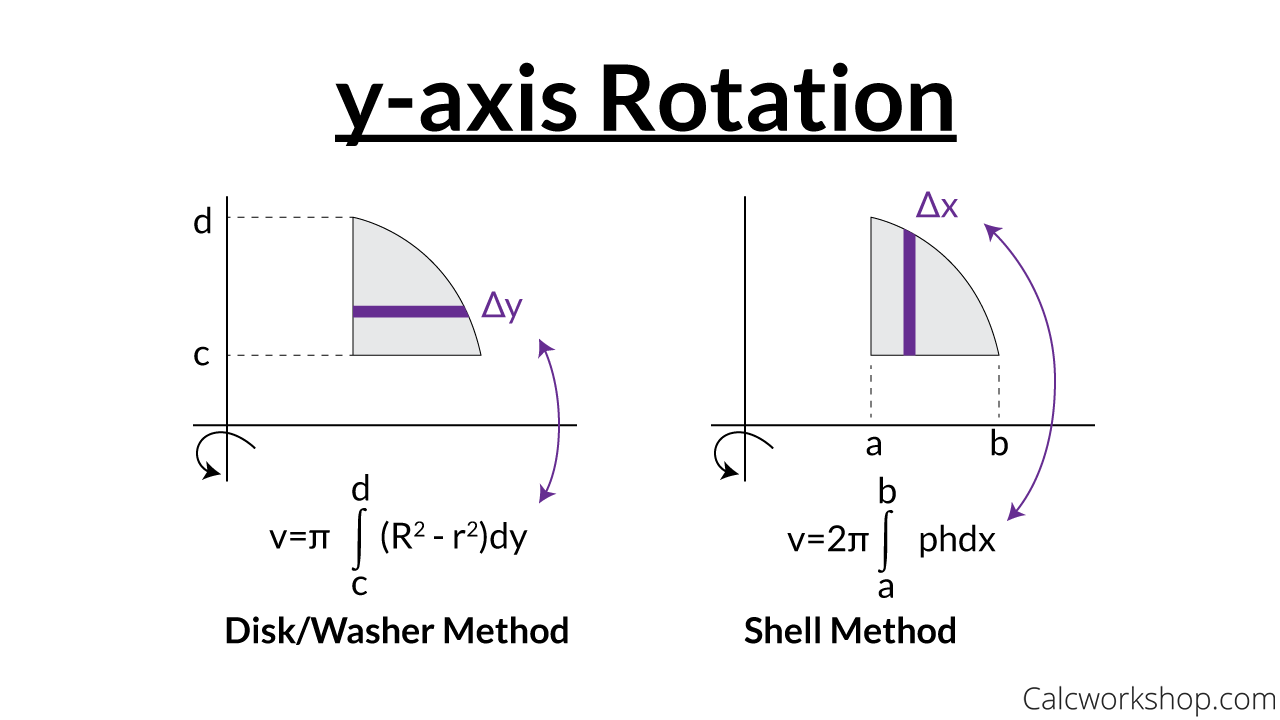
There are a couple of important differences between this method and the method of rings/disks that we should note before moving on. First, rotation about a vertical axis (i.e. $y=n$) will give an area that is a function of $x$ and rotation about a horizontal axis (i.e. $x=k$) will give an area that is a function of $y$. This is exactly opposite of the method of rings/disks. Second, we don’t take the complete range of x or y for the limits of integration as we did in the previous section. Instead we take a range of x or y that will cover one side of the solid. As we noted in the first example if we expand out the radius to cover one side we will automatically expand in the other direction as well to cover the other side.

Rotated about the y-axis $2\pi \IntegrateFor{a}{b}{x \cdot f(x)}{x}$
Rotated about the x-axis: $2\pi \IntegrateFor{a}{b}{y \cdot f(y)}{y}$

Volumes by Cylindrical Shells - General Formulas

Cylindrical Shells Across $x=n$

$$\begin{equation} \begin{split} A(x) &= 2\pi \; \overbrace{\left(\text{radius}\right)}^{n - x \; \text{or} \; x} \; \left(\text{height}\right) \end{split} \end{equation}$$

Chapter 5 | Applications of Integration

§5.1 | Areas Between Curves

§5.2 | Volumes

Solids of revolution

Cross-sectional Area

Disk Function Examples

Washer Function Examples

§5.3 | Volumes by Cylindrical Shells

The Shell Method

Significant Distinction

Alternatively

Summary of §5.2 and §5.3

Volumes by Cylindrical Shells - General Formulas

Cylindrical Shells Across \(x=n\)

§5.4 | Work

§5.5 | Average Value of a Function