Chapter 3 | Trigonometric Identities and Equations

Navigation

§3.1 | Verification of Trigonometric Identities

§3.2 | Sum, Difference, and Cofunction Identities

Sum and Difference Identities

\[\begin{equation} \begin{split} \cos(\alpha - \beta) &= \cos(\alpha) \cdot \cos(\beta) + \sin(\alpha) \cdot \sin(\beta) \\ \cos(\alpha + \beta) &= \cos(\alpha) \cdot \cos(\beta) - \sin(\alpha) \cdot \sin(\beta) \\ &\\ \sin(\alpha - \beta) &= \sin(\alpha) \cdot \cos(\beta) - \cos(\alpha) \cdot \sin(\beta) \\ \sin(\alpha + \beta) &= \sin(\alpha) \cdot \cos(\beta) + \cos(\alpha) \cdot \sin(\beta) \\ &\\ \tan(\alpha + \beta) &= \frac{\tan(\alpha) + \tan(\beta)}{1 - \tan(\alpha) \cdot \tan(\beta)} \\ \tan(\alpha - \beta) &= \frac{\tan(\alpha) - \tan(\beta)}{1 + \tan(\alpha) \cdot \tan(\beta)} \end{split} \end{equation}\]

Cofunction Identities

\[\begin{equation} \begin{split} \sin(\theta) &= \cos(\frac{1}{4}\tau - \theta) \\ \cos(\theta) &= \sin(\frac{1}{4}\tau - \theta) \\ \tan(\theta) &= \cot(\frac{1}{4}\tau - \theta) \\ &\\ \cot(\theta) &= \tan(\frac{1}{4}\tau - \theta) \\ \csc(\theta) &= \sec(\frac{1}{4}\tau - \theta) \\ \sec(\theta) &= \csc(\frac{1}{4}\tau - \theta) \end{split} \end{equation}\]

§3.3 | Double- and Half-Angle Identities

Double-Angle Identities

Remember for Exams. The professor said this isn’t given during the Exam, and that we need to know this, said this in the context of Double-Angle & Half-Angle Identities.
The Double-Angle Identities are easy to derive from the Sum and Difference Identities.

\begin{equation} \begin{split} \sin(2\alpha) &= 2\sin(\alpha)\cos(\alpha) \\ \cos(2\alpha) &= \cos^2(\alpha) - \sin^2(\alpha) \\ &= 1 - 2\sin^2(\alpha) \\ &= 2\cos^2(\alpha) - 1 \\ &\\ \tan(2\alpha) &= \frac{2\tan(\alpha)}{1 - \tan^2(\alpha)} \end{split} \end{equation}

Half-Angle Identities

Remember for Exams. The professor said this isn’t given during the Exam, and that we need to know this, said this in the context of Double-Angle & Half-Angle Identities, she may have been talking about just the Double-Angle Identities.

\[\begin{equation} \begin{split} \sin \frac{\alpha}{2} &= \pm \sqrt{\frac{1 - \cos(\alpha)}{2}} \\ \cos \frac{\alpha}{2} &= \pm \sqrt{\frac{1 + \cos(\alpha)}{2}} \\ \tan \frac{\alpha}{2} &= \pm \sqrt{\frac{1 - \cos(\alpha)}{1 + \cos(\alpha)}} = \frac{sin(\alpha)}{1 + \cos(\alpha)} = \frac{1 - \cos(\alpha)}{sin(\alpha)} \end{split} \end{equation}\]

Warning

The choice of the ± sign depends on the quadrant in which \(\frac{\alpha}{2}\) lies.

Power-Reducing Identities

\[\begin{equation} \begin{split} \sin^2(\alpha) &= \frac{1 - \cos(2\alpha)}{2} \\ &\\ \cos^2(\alpha) &= \frac{1 + \cos(2\alpha)}{2} \\ &\\ \tan^2(\alpha) &= \frac{1 - \cos(2\alpha)}{1 + \cos(2\alpha)} \end{split} \end{equation}\]

§3.4 | Identities Involving the Sum of Trigonometric Functions

Product-to-Sum Identities

\begin{equation} \begin{split} \sin(\alpha) \cdot \cos(\beta) &= \frac{1}{2} \Big[ \sin(\alpha + \beta) + \sin(\alpha - \beta) \Big] \\ \cos(\alpha) \cdot \sin(\beta) &= \frac{1}{2} \Big[ \sin(\alpha + \beta) - \sin(\alpha - \beta) \Big] \\ \cos(\alpha) \cdot \cos(\beta) &= \frac{1}{2} \Big[ \cos(\alpha + \beta) + \cos(\alpha - \beta) \Big] \\ \sin(\alpha) \cdot \sin(\beta) &= \frac{1}{2} \Big[ \cos(\alpha - \beta) - \cos(\alpha + \beta) \Big] \end{split} \end{equation}

Sum-to-Product-Identities

\begin{equation} \begin{split} \sin(x) + \sin(y) &= 2 \cdot \sin\left( \frac{x + y}{2} \right) \cdot \cos\left( \frac{x - y}{2} \right) \\ \cos(x) + \cos(y) &= 2 \cdot \cos\left( \frac{x + y}{2} \right) \cdot \cos\left( \frac{x - y}{2} \right) \\ \sin(x) - \sin(y) &= 2 \cdot \cos\left( \frac{x + y}{2} \right) \cdot \sin\left( \frac{x - y}{2} \right) \\ \cos(x) - \cos(y) &= -2 \sin \cos\left( \frac{x + y}{2} \right) \cdot \sin\left( \frac{x - y}{2} \right) \end{split} \end{equation}

§3.5 | Inverse Trigonometric Functions

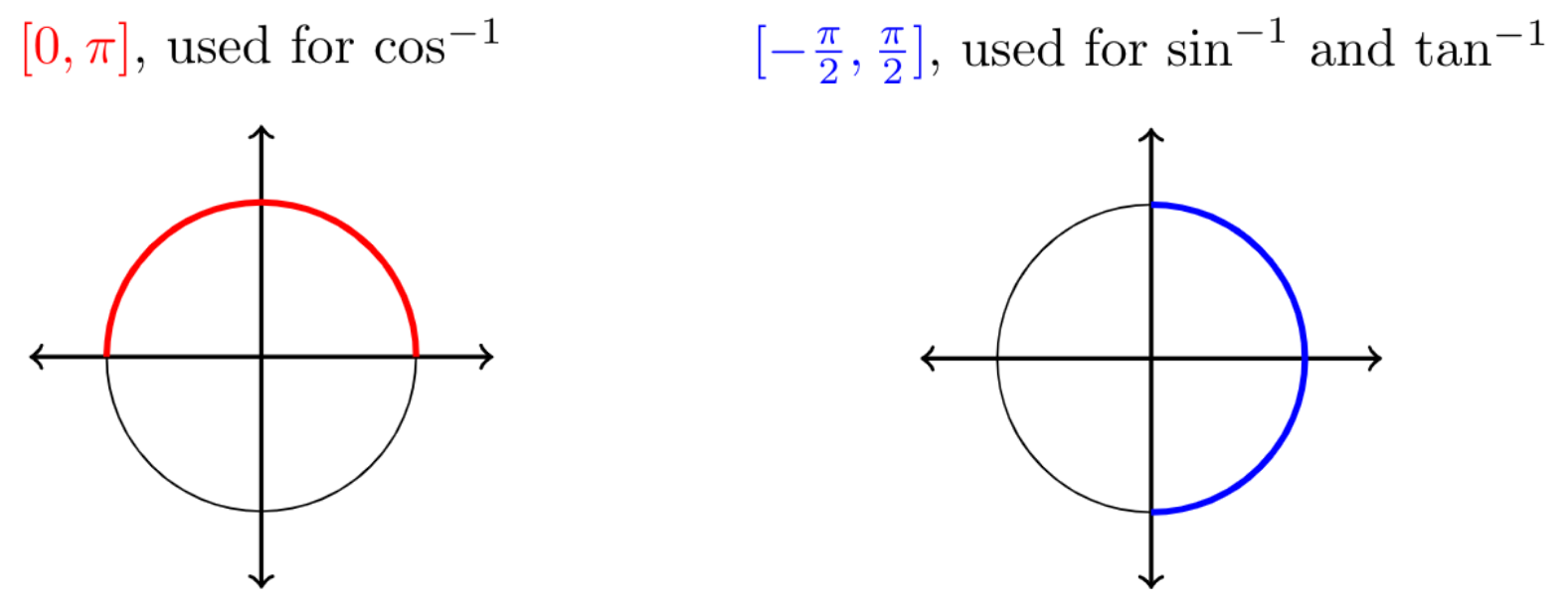
range inverse trig

Definition of \(\arcsin(x)\)

\[y = \arcsin(x)\]

if and only if

\[x = \sin(y)\]

where

\[-1 \leq x \leq 1 \\ -\frac{1}{4}\tau \leq y \leq \frac{1}{4}\tau\]

The graph of \(y=\sin\;x\) with \(x\) restricted to to \(\left\lbrack -\frac{\tau}{4},\frac{\tau}{4} \right\rbrack\):

Definition of \(\arccos(x)\)

\[y = \arccos(x)\]

if and only if

\[x = \cos(y)\]

where

\[-1 \leq x \leq 1 \\ 0 \leq y \leq \pi\]

The graph of \(y=\cos\;x\) with \(x\) restricted to to \(\left\lbrack 0,\frac{1}{2}\tau \right\rbrack\):

Warning

The choice of ranges for \(\arcsin(x)\) and \(\arccos(x)\) is not universally accepted.

Identities for the Inverse Secant, Cosecant, and Cotangent Functions

\[\begin{equation} \begin{aligned} \sin^{-1}\frac{1}{x} &= \csc^{-1}x & \text{if}\; & -1 \leq x \leq 1 \\ &\\ \cos^{-1}\frac{1}{x} &= \sec^{-1}x & \text{if}\; & -1 \leq x \leq 1 \\ &\\ \frac{\pi}{2} - \tan^{-1}x &= \cot^{-1}x & \text{if}\; & x \in \mathbf{R} \\ \end{aligned} \end{equation}\]

Composition of Trigonometric Functions and Their Inverses

\[\begin{equation} \begin{aligned} \sin \circ \arcsin \triangleleft \; x &= x & \text{if}\; & -1 \leq x \leq 1 \\ &\\ \cos \circ \arccos \triangleleft \; x &= x & \text{if}\; & -1 \leq x \leq 1 \\ &\\ \tan \circ \arctan \triangleleft \; x &= x & \text{if}\; & x \in \mathbf{R} \\ &\\ \arcsin \circ \sin \triangleleft \; x &= x & \text{if}\; & -\frac{1}{4}\tau \leq x \leq \frac{1}{4}\tau \\ &\\ \arccos \circ \cos \triangleleft \; x &= x & \text{if}\; & 0 \leq x \leq \pi \\ &\\ \arctan \circ \tan \triangleleft \; x &= x & \text{if}\; & -\frac{1}{4}\tau \leq x \leq \frac{1}{4}\tau \end{aligned} \end{equation}\]

Where \(x \in \mathbf{R}\) means if x is any real number.